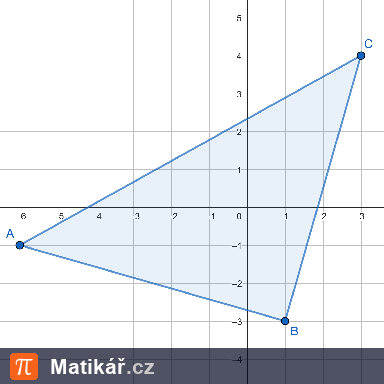
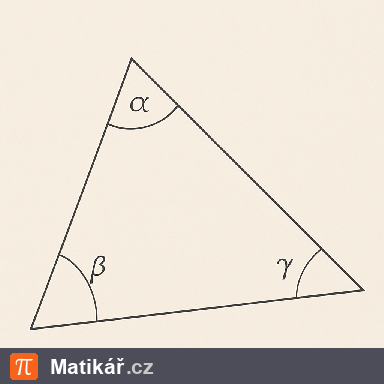
V trojúhelníku je vnitřní úhel \( \beta \) o 20 ° menší než úhel \( \alpha \) a úhel \( \gamma \) je třikrát větší než úhel \( \beta \).

V trojúhelníku je vnitřní úhel \(\beta\) o 20° menší než úhel \(\alpha\) a úhel \(\gamma\) je třikrát větší než úhel \(\beta\).

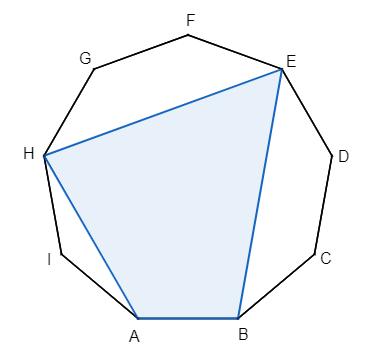
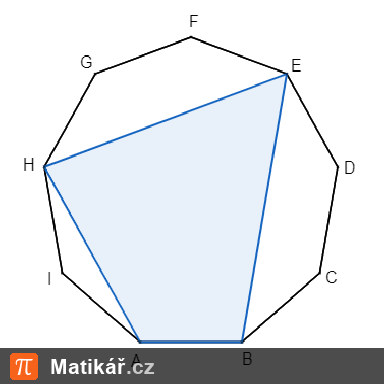
Je dán pravidelný devítiúhelník ABCDEFGHI.


Adam měl o dvě sedminy více jablek než Eva. Dohromady měli 320 jablek.

O úhlech v lichoběžníku ABCD je známo: velikost úhlu \( \gamma \) je 121 °, velikost úhlu \( \alpha \) je 2/3 úhlu \( \delta \).

Hlídka měla určený pochodový úhel 13 °. Po ujetí 9 km se úhel změnil na 62 °. Tímto směrem šla hlídka 10 km.

Trojúhelník spojuje na ciferníku cifry 2, 7 a 9.

Je dán lichoběžník ABCD (AB||CD):
|AB| = 7 cm
|BC| = 3,50 cm
|CD| = 4 cm
A velikost úhlu ABC = 60°



Je dán pravidelný šestiúhelník ABCDEF.

Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,30 m. Odchylka strany od roviny podstavy je 36 °.

Velikosti vnitřních úhlů α, β, γ trojúhelníku jsou v poměru 3:4:5.
Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15 °.

Tři vnitřní úhly čtyřúhelníku mají velikosti 65 °, 110 °, 140 °.

V trojúhelníku ABC je velikost vnitřního úhlu \( \beta \) o 10 stupňů větší než velikost úhlu \( \alpha \) a velikost úhlu \( \gamma \) je 3× větší než velikost úhlu \( \beta \).
