Matikář - Úlohy na procvičení

Úlohy: 121–140 / 190

Řešte nerovnice v R

a) $x^2-4x-21 \geq 0$

b) $x^2-36 \leq 0$

c) $-x^2+x+20 > 0$

d) $x^2-6x+9 < 0$

e) $x^2+1 \geq 0$

f) $-x^2-5 \leq 0$

g) $x^2-2x+1 \leq 0$

h) $2x^2+5x-3 \geq 0$

Řešení

a) $x \in \left ( - \infty ; -3 \right \rangle \cup \left \langle 7; \infty \right )$

b) $x \in \left \langle -6; 6 \right \rangle$

c) $x \in \left ( -4; 5 \right )$

d) nemá řešení v R

e) $x \in \left ( -\infty; \infty \right )$

f) $x \in \left ( -\infty; \infty \right )$

g) $x = 1$

h) $x \in \left ( - \infty ; -3 \right \rangle \cup \left \langle \frac{1}{2}; \infty \right )$

Matematická úloha – Kvadratické nerovnice

122. Kvadratické nerovnice

Řešte nerovnice

a) $\left (2x - 2 \right )^2-3x \left (x-3 \right ) \leq 19-x$

b) $\left (2 - 3x \right ) - \left (x - 1 \right ) \geq - 4 - \left (x-1 \right )^2$

c) $-2 \left (x^2 - 1 \right ) + 2 \left (1 - x \right ) - 5 \leq 0$

d) $x^2 - 3x + 7 > 5x + 16$

e) $x^2-\left (x - 1 \right )^2 > x \left (x - 1 \right ) + 1$

f) $\left (x + 1 \right )^2 - 2 \left (x + 1 \right ) + 1 \leq 0$

Řešení

a) $x \in \left \langle -5; 3 \right \rangle$

b) $x \in \left ( - \infty ; 2 \right \rangle \cup \left \langle 4; \infty \right )$

c) $x \in \left ( - \infty ; \infty \right )$

d) $x \in \left ( - \infty ; -1 \right ) \cup \left ( 9; \infty \right )$

e) $x \in \left ( 1 ; 2 \right )$

f) $x \in \left \{0\right \}$

123. Graf kvadratické funkce

Graf kvadratické funkce prochází body A[1;1], B[3;-1] a C[1;2].

Určete obecnou rovnici této kvadratické funkce.

Řešení

$ y=2,5x^{2}-9.5x+8 $

Matematická úloha – Graf kvadratické funkce

124. Nerovnice

Řešte nerovnice

a) $\frac{2x-3}{3}+\frac{3x-2}{2}\geq\frac{1}{6}$

b) $\frac{2x+1}{3}<\frac{2x-1}{5}$

c) $\frac{2x-1}{3}-\frac{x+6}{2}<0$

d) $\frac{x+1}{4}-\frac{x-1}{2}-3<\frac{2x-1}{2}$

e) $\frac{2x-17}{4}-\frac{8-x}{2}-2\leq x-4+\frac{x}{8}$

f) $\frac{x-5}{3}+2\leq \frac{2-x}{5}$

Řešení

a) $x \in \left \langle 1;\infty \right )$

b) $x \in \left (-\infty; -2 \right )$

c) $x \in \left (-\infty; 20 \right )$

d) $x \in \left (-\frac{7}{5}; \infty \right )$

e) $x \in \left \langle -50;\infty \right )$

f) $x \in \left (-\infty; \frac{1}{8} \right \rangle$

125. Rovnice

Řešte rovnice a určete, pro jaké x nemají rovnice smysl.

a) $\frac{11+3x}{x+3}-\frac{5x}{x-4}+\frac{x}{x^{2}-x-12}+2=0$

b) $\frac{1}{x+4}+\frac{x^{2}-20}{x^{2}-16}=1$

c) $\frac{2x}{x+3}-\frac{2x}{x-3}=\frac{72}{4x^{2}-36}$

d) $\frac{2x-1}{2x+1}=\frac{2x+1}{2x-1}+\frac{8x}{1-4x^{2}}$

Řešení

a) $K=\left \{ -4 \right \}; x\neq -3\vee x\neq 4$

b) $K=\left \{ 8 \right \}; x\neq \pm{4}$

c) $K=\left \{ -\frac{3}{2} \right \}; x\neq \pm{3}$

d) $K= \mathbb{R} \setminus \left\{ -\frac{1}{2}, \frac{1}{2} \right\}$

126. Rovnice

Řešte rovnici a určete, pro jaké x nemá rovnice smysl.

$\frac{12x^{2}+30x-21}{16x^{2}-9}=\frac{3x-7}{3-4x}+\frac{6x+5}{4x+3}$

Řešení

$K=\left \{ 3 \right \}; x\neq \pm{\frac{3}{4}}$

127. Rovnice

Řešte rovnice a určete, pro jaké x nemají rovnice smysl.

a) $x-3+\frac{1}{x-2}=x-4-\frac{2x-3}{2-x}$

b) $\frac{1}{x-3}-\frac{1}{x+2}=\frac{5}{x^{2}+6}$

c) $\frac{5}{2x-3}-\frac{3x-8}{4x-6}=\frac{7}{9}-\frac{6x-1}{10x-15}$

d) $\frac{5}{2x-3}+\frac{3x+8}{4x-6}=\frac{7}{6}-\frac{6x-2}{10x-15}$

Řešení

a) $K=\left \{ \right \}; x\neq \2$

b) $K=\left \{ -12 \right \}; x\neq 3\vee x\neq -2$

c) $K=\left \{ 6 \right \}; x\neq \frac{3}{2}$

d) $K=\left \{ -33 \right \}; x\neq \frac{3}{2}$

128. Rovnice

Řešte rovnice a určete, pro jaké x nemají rovnice smysl.

a) $5+\frac{3}{3x-12}=\frac{5-x}{x-4}$

b) $\frac{7x+2}{3x-2}-\frac{9}{4-6x}=\frac{10x-4}{9x-6}-\frac{1}{16}$

c) $\frac{4}{(x-1)(x+3)}+\frac{x+1}{x-1}=\frac{x+2}{x+3}$

d) $\frac{3}{(2x+5)^{2}}+\frac{4}{(2x+1)^{2}}=\frac{7}{(2x+5)(2x+1)}$

Řešení

a) $K=\left \{ \right \}; x\neq 4$

b) $K=\left \{ -2 \right \}; x\neq \frac{2}{3}$

c) $K=\left \{ \right \}; x\neq -1\vee x\neq -3$

d) $K=\left \{ -\frac{17}{2} \right \}; x\neq -\frac{5}{2}\vee x\neq-\frac{1}{2}$

129. Rovnice

Řešte rovnice a určete, pro jaké x nemají rovnice smysl.

a) $\frac{2}{(1-3x)(3x+11)}=\frac{1}{(3x-1)^{2}}-\frac{3}{(3x+11)^{2}}$

b) $\frac{1}{x-2}-\frac{x-3}{x+4}=\frac{6}{x^{2}+2x-8}-1$

c) $\frac{x+1}{x-1}+\frac{2}{x+2}-1=\frac{6}{x^{2}+x-2}$

d) $1+\frac{2x}{x+4}-\frac{15}{2x^{2}+7x-4}=\frac{6x}{2x-1}$

Řešení

a) $K=\left \{ -\frac{2}{3} \right \}; x\neq \frac{1}{3}\vee x\neq -\frac{11}{3}$

b) $K=\left \{ \right \}; x\neq 2\vee x\neq -4$

c) $K=\left \{ \right \}; x\neq 1\vee x\neq -2$

d) $K=\left \{ -1 \right \}; x\neq -4\vee x\neq\frac{1}{2}$

130. Nerovnice

Řešte nerovnice v R

a) $\frac{2x-3}{4}+\frac{x}{2}<1$

b) $\frac{2x-1}{2}-23<2x-20$

c) $\frac{3x-1}{4}+\frac{5-6x}{2}\leq 9+\frac{3x}{2}$

d) $3(x+2)+\frac{x-2}{2}<0$

e) $3(x-2)+\frac{x-2}{2}\geq0$

f) $\frac{3x-1}{4}-\frac{4x-1}{6}<\frac{1}{2}$

Řešení

a) $x \in \left ( -\infty; \frac{7}{4} \right )$

b) $x \in \left ( -\frac{7}{2};\infty \right )$

c) $x \in \left \langle -\frac{9}{5};\infty \right )$

d) $x \in \left ( -\infty; -\frac{10}{7} \right )$

e) $x \in \left \langle 2;\infty \right )$

f) $x \in \left ( -\infty; 7 \right )$

131. Rovnice

Řešte rovnice a určete, pro jaké x nemají rovnice smysl.

a) $\frac{3x+1}{5x-2}=\frac{2(3x+14)}{5(2x+7)}$

b) $\frac{x+1}{x+3}=\frac{x+5}{x+9}$

c) $\frac{3}{2}-\frac{10+x}{2x}=0$

d) $\frac{2x+3}{4x-5}+\frac{2-x}{5-4x}=1$

Řešení

a) $K=\left \{ 7 \right \}; x\neq \frac{2}{5}\vee x\neq -\frac{7}{2}$

b) $K=\left \{ 3 \right \}; x\neq -3\vee x\neq -9$

c) $K=\left \{ 5 \right \}; x\neq 0$

d) $K=\left \{ 6 \right \}; x\neq \frac{5}{4}$

132. Střed úsečky

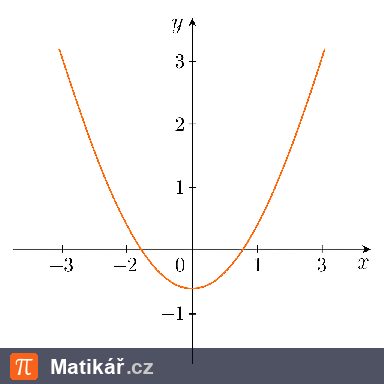
Jsou dány dva body A[a₁, 4] a B[7, -2]. Úsečka AB má střed, jehož obě souřadnice jsou stejné.

Vypočítejte souřadnici a₁.

Řešení

a₁ = -5

133. Aritmetická posloupnost

V aritmetické posloupnosti je dáno a₁ = 4, S_n = 589, d = 3.

Vypočtěte, kolik členů má aritmetická posloupnost.

Řešení

Aritmetická posloupnost má 19 členů.

Matematická úloha – Aritmetická posloupnost

134. Červené a bílé kuličky

Máme 15 červených a 5 bílých kuliček.

Vypočítejte v procentech, jaká je pravděpodobnost, že první vytažená kulička bude bílá.

Řešení

Pravděpodobnost, že první vytažená kulička bude bílá, je 25 %.

Matematická úloha – Červené a bílé kuličky

135. Pěticiferná čísla

Jsou dané cifry 0, 1, 3, 4, 7.

Určete počet všech přirozených pěticiferných čísel, v nichž je každá z číslic alespoň jednou obsažena.

Řešení

Jde o 96 čísel.

136. Počet čísel

Určete počet všech přirozených čísel větších než 2 000 , ve kterých se vyskytují číslice 1, 2, 4, 6, 8, a to každá nejvíce jednou.

Řešení

216

137. Počet přirozených čísel

Určete počet všech přirozených čísel větších než 200, ve kterých se vyskytují číslice 1, 2, 4, 6, 8, a to každá nejvíce jednou.

Řešení

288

Matematická úloha – Počet přirozených čísel

138. Rotace trojúhelníku

Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a = 2 cm kolem jedné z jeho stran.

Vypočítejte v cm³ objem tohoto rotačního tělesa. (Zaokrouhlete na dvě desetinná místa.)

Řešení

Objem je 6,28 cm³.

250 studentů skládalo zkoušky z programování, matematiky a fyziky. 124 studentů složilo zkoušku z programování, 60 studentů udělalo zkoušku z matematiky a 51 studentů udělalo zkoušku z fyziky. Zkoušku z programování i matematiky udělalo 19 studentů, z matematiky i fyziky 20 studentů a z programování i fyziky 16 studentů. Všechny tři zkoušky udělalo 8 studentů.

Vypočítejte, kolik studentů nesložilo ani jednu zkoušku.

Řešení

Ani jednu zkoušku neudělalo 30 studentů.

140. Taneční

Do taneční přišlo 32 chlapců a 34 dívek.

Vypočítejte, kolik různých tanečních párů mohou vytvořit.

Řešení

Mohou vytvořit 1 088 tanečních párů.

5 678 9

Střední škola

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení