Úlohy: 161–180 / 190

678910
Přehled ročníků

161. Kinetická energie auta

Auto o hmotnosti 1 850 kg zvětšilo svoji rychlost z 27 na 81 km/h.

Vypočtěte, o joulů kolik se zvětšila jeho kinetická energie.
Řešení
Kinetická energie se zvětšila o 416 250 joulů.
Matematická úloha – Kinetická energie auta

162. Tříčlenná družstva

Ze čtyř dívek a čtyř chlapců má být vytvořeno jedno tříčlenné družstvo, ve kterém bude jedna dívka a dva chlapci.

Vypočtěte, kolika různými možnostmi lze družstvo vytvořit.
Řešení
Družstvo lze vytvořit 24 způsoby.
Matematická úloha – Tříčlenná družstva

163. Stavba zdi

Zedník s učedníkem by společně postavili zeď za 15 hodin. Učedník sám by zeď postavil za 60 hodin.

Vypočtěte,
a)   za kolik hodin by zeď stavěl sám zedník,
b)   o kolik procent se zkrátí doba stavby zdi při zapojení učedníka oproti době práce samotného zedníka.
Řešení
a)   Zedník sám by stavěl zeď 20 hodin.
b)   Doba se zkrátí o 25 %.
Matematická úloha – Stavba zdi

164. Kružnice určené body

V rovině je 10 různých bodů.

Vypočtěte, kolik nejvíce kružnic je těmito body určeno.
Řešení
Těmito body je určeno 120 kružnic.
Matematická úloha – Kružnice určené body

165. Vyřešte rovnici

Vyřešte v R rovnice
a)   
b)   
c)   
d)   
Řešení
a)   x = 0
b)   x = –2
c)   x = –2
d)   nemá řešení
Matematická úloha – Vyřešte rovnici

166. Kuželovitá střecha

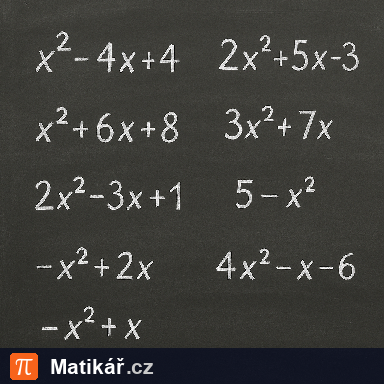
Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,30 m. Odchylka strany od roviny podstavy je 36 °.

Vypočtěte v m2 spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. (Výsledek zapište na dvě desetinná místa.)
Řešení
Spotřeba plechu je 19,40 m2
Matematická úloha – Kuželovitá střecha

167. Těžiště trojúhelníku

V trojúhelníku ABCE prochází přímka p těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC.

Vypočtěte poměr obsahu rozdělené menší části trojúhelníku přímkou ​​p a obsahu trojúhelníku.
Řešení
Poměr je 4:9.
Matematická úloha – Těžiště trojúhelníku

168. Řešte rovnice

Řešte v R rovnice
a)   
b)   
c)   
d)   
Řešení
a)   x = 7
b)   x = 2
c)   x = 7
d)   x = 6
Matematická úloha – Řešte rovnice

169. Vyřešte v R rovnici

Vyřešte v R rovnice
a)   
b)   
c)   
d)   
Řešení
a)   x = 2
b)   x = 7
c)   x = 6
d)   x = -3
Matematická úloha – Vyřešte v R rovnici

170. Rovnice v podílovém tvaru

Řešte v R rovnice
a)   
b)   
c)   
d)   
Řešení
a)   x = 2
b)   x = 1
c)   x = -3
d)   x = -1
Matematická úloha – Rovnice v podílovém tvaru

171. Pastelky

V penálu je 5 pastelek: modrá, žlutá, zelená, červená a fialová.

Vypočtěte,
a)   kolik je různých možností uložení v penálu,
b)   kolik je různých možností uložení v penálu za předpokladu, že modrá a žlutá musí být (v tomto pořadí) vždy vedle sebe.
Řešení
a)   Je 120 možností.
b)   Je 24 možností.
Matematická úloha – Pastelky

172. Dělení bonbónů

Jana, Martina a Zuzka si rozdělily bonbóny v poměru 3:7:5 . Martina dostala o 9 bonbonů méně než měly Jana a Zuzka spolu.

U každého z následujících tvrzení rozhodněte, zda je pravdivé, či nikoliv.
a)   Martina dostala méně bonbonů než Zuzka.
b)   Všechny spolu dostaly 135 bonbonů.
c)   Martina dostala o 16 bonbonů více než Zuzka.
d)   Zuzka dostala nejvíce bonbonů.
Řešení
a)   0
b)   1
c)   0
d)   0
Matematická úloha – Dělení bonbónů

173. Modré a červené kuličky

Máme 2 stejné modré kuličky a 2 stejné červené kuličky. Uspořádáme je všemi způsoby do řady.

Vypočtěte, kolik různých uspořádání existuje.
Řešení
Existuje 6 uspořádání.
Matematická úloha – Modré a červené kuličky

174. Kuličky různých barev

Máme 6 kuliček různých barev. Najednou vybereme dvě kuličky.

Vypočtěte, kolik existuje možností.
Řešení
Existuje celkem 15 možností.
Matematická úloha – Kuličky různých barev

175. Dělitelnost pěti

Zapište zlomkem v základním tvaru pravděpodobnost, že náhodné dvojciferné číslo:
a)   je dělitelné pěti,
b)   není dělitelné pěti.
Řešení
a)   p1 = 1/5
b)   p2 = 4/5
Matematická úloha – Dělitelnost pěti

176. Koule v osudí

V osudí je 5 bílých a 9 černých koulí. Namátkou vybereme tři koule.

Zapište číslem na čtyři desetinná místa pravděpodobnost, že…
a)   …vybrané koule nebudou stejné barvy,
b)   …mezi nimi budou aspoň dvě černé.
Řešení
a)   p1 = 0,74
b)   p2 = 0,73
Matematická úloha – Koule v osudí

177. Střelba na terč

Terč je rozdělen na tři pásma. Pravděpodobnost, že střelec zasáhne první pásmo, je 0,18, druhé pásmo 0,20, třetí pásmo 0,44.

Číslem na dvě desetinná místa zapište pravděpodobnost, že střelec
a)   zasáhne terč,
b)   mine terč.
Řešení
a)   p1 = 0,82
b)   p2 = 0,18
Matematická úloha – Střelba na terč

178. Házení kostkou

Zapište zlomkem v základním tvaru, jaká je pravděpodobnost, že při hodu kostkou:
a)   padne číslo větší než 4,
b)   nepadne číslo větší než 4.
Řešení
a)   p1 = 1/3
b)   p2 = 2/3
Matematická úloha – Házení kostkou

179. Peníze v pokladničce

Karel má v pokladničce celkem 19 mincí, a to pouze desetikorunové a padesátikorunové mince. Celkem má v pokladničce naspořeno 830 Kč.

O každém z následujících tvrzení rozhodněte, jestli je pravdivé či nikoliv.
a)   V pokladničce chybí 170 Kč do tisíce.
b)   V pokladničce je méně desetikorun než padesátikorun.
c)   V pokladničce je o 13 padesátikorun více než desetikorun.
d)   V pokladničce je stejný počet desetikorun a padesátikorun.
e)   V pokladničce jsou desetikoruny a padesátikoruny v poměru 3 : 16 (v tomto pořadí).
Řešení
a)   0
b)   0
c)   0
d)   1
e)   0
Matematická úloha – Peníze v pokladničce

180. Uskladněné brambory

Firma má dva sklady brambor. V prvním skladu je třikrát více brambor než ve druhém. Z prvního skladu byla odvezena polovina zde uskladněného množství brambor a zbylo v něm o 90 tun brambor více než ve druhém skladu.

Vypočtěte,
a)   kolik tun brambor má firma uskladněno v druhém skladu brambor,
b)   kolik tun brambor bylo odvezeno z prvního skladu.
Řešení
a)   Ve druhém skladu je 180 tun brambor.
b)   Z prvního skladu bylo odvezeno 270 tun brambor.
Matematická úloha – Uskladněné brambory
 
678910