Matikář - Úlohy na procvičení

Úlohy: 101–120 / 190

Narýsujte graf funkce:

a) $y=\left (\frac{x}{4}\right )^{2}-\left |\left(\frac{x}{2}+1\right )^{2}-1\right |$

b) $y=\left |\left (x-1\right )^{2}-1\right |-\left(\frac{x}{2}\right )^{2}$

c) $y=\left |x^{2}-x-2\right |-x^{2}$

Řešení

Matematická úloha – Kvadratické funkce s absolutní hodnotou

102. Lineární funkce s absolutní hodnotou

Narýsujte graf funkce:

a) $y=\left |4-2x\right |+x-1$

b) $y=\left |x-2\right |-2$

c) $y=\frac{x}{2}+3-\left |x-2\right |$

d) $y=2x-3-\left |x-2\right |$

Řešení

Matematická úloha – Lineární funkce s absolutní hodnotou

103. Průměry tří čísel

Jsou dána tři navzájem různá čísla. Průměr průměru dvou menších čísel a průměr dvou větších čísel je roven průměru všech tří čísel. Průměr nejmenšího a největšího čísla je 2 022

Určete součet tří daných čísel.

Řešení

Součet tří daných čísel je 6 066.

104. Kvadratické nerovnice

Řešte v R nerovnice:

a) $x^{2}+13x+36\geq0$

b) $x^{2}-14x+45\leq0$

c) $x^{2}-5x\leq0$

d) $x^{2}+7x+12>0$

e) $x^{2}+4x-45<0$

f) $x^{2}-16<0$

g) $x^{2}+8x+16<0$

h) $x^{2}+20x+100\geq0$

Řešení

a) $x \in \left ( -\infty; -9\right \rangle \cup \left \langle-4; \infty; \right )$

b) $x \in \left \langle 5; 9 \right \rangle$

c) $x \in \left \langle 0; 5 \right \rangle$

d) $x \in \left ( -\infty; -4\right ) \cup \left (-3; \infty; \right )$

e) $x \in \left ( -9; 5 \right )$

f) $x \in \left ( -4; 4 \right )$

g) nemá řešení v R

h) $x \in \left ( -\infty; \infty; \right )$

Matematická úloha – Kvadratické nerovnice

105. Funkce s absolutní hodnotou

Narýsujte graf funkce.

a) $y=\left | x-4 \right |-\left | x-4 \right |+x$

b) $y=\left | 4-x \right |-\left | 2-x \right |$

c) $y=\left | -x \right |-\left | 2-\frac{x}{2} \right |$

d) $y=\left | x-4 \right |+\left | x \right |-6$

Řešení

Matematická úloha – Funkce s absolutní hodnotou

106. Rovnice lineární funkce

Jsou dány dva body.

Určete rovnici lineární funkce procházející těmito body.

a) A[–2;–5], B[2;1]

b) A[–4;1], B[3;1]

c) A[–3;6], B[6;3]

d) A[–1;4], B[2;7]

e) A[–1;–7], B[4;3]

f) A[–1;–2], B[–1;0]

g) A[-3;6], B[0;3]

h) A[–1;–3], B[2;6]

Řešení

a) $y=\frac{3}{2}x-2$

b) $y=1$

c) $y=-\frac{x}{3}+5$

d) $y=x+5$

e) $y=2x-5$

f) nemá řešení

g) $y=-x+3$

h) $y=3x$

Matematická úloha – Rovnice lineární funkce

107. Vlastnosti funkce

Je dána funkce f: $y = 2x+3$

Určete:

a) definiční obor funkce f

b) obor hodnot funkce f

c) průsečík grafu funkce f s osou y (pokud existuje)

d) průsečíky grafu funkce f s osou x (pokud existují)

e) zda je funkce f sudá nebo lichá

f) v kterých intervalech funkce f roste

g) v kterých intervalech funkce f klesá

h) zda je funkce f prostá

i) inverzní funkci k funkci f

j) načrtněte graf funkce

Řešení

a) Definiční obor funkce je $D_{f}=R$

b) Obor hodnot funkce je $H_{f}= R$

c) Průsečík s osou y je $P_{y} \left [0;3 \right ]$

d) Průsečík s osou x je $P_{x} \left [-\frac{3}{2};0 \right ]$

e) Funkce f není ani sudá ani lichá

f) Funkce f je rostoucí v intervalu $\left ( -\infty; \infty \right )$

g) Funkce f není klesající.

h) Funkce f je prostá.

i) Inverzní funkce k funkci f je $y=\frac{1}{2}x-\frac{3}{2}.$

108. Vlastnosti funkce

Je dána funkce f: $y = \frac{1}{2}x-2$

Určete:

a) definiční obor funkce f

b) obor hodnot funkce f

c) průsečík grafu funkce f s osou y (pokud existuje)

d) průsečíky grafu funkce f s osou x (pokud existují)

e) zda je funkce f sudá nebo lichá

f) v kterých intervalech funkce f roste

g) v kterých intervalech funkce f klesá

h) zda je funkce f prostá

i) inverzní funkci k funkci f

j) načrtněte graf funkce

Řešení

a) Definiční obor funkce je $D_{f}=R$

b) Obor hodnot funkce je $H_{f}= R$

c) Průsečík s osou y je $P_{y} \left [0;-2 \right ]$

d) Průsečík s osou x je $P_{x} \left [4;0 \right ]$

e) Funkce f není ani sudá ani lichá

f) Funkce f je rostoucí v intervalu $\left ( -\infty; \infty \right )$

g) Funkce f není klesající.

h) Funkce f je prostá.

i) Inverzní funkce k funkci f je $y=2x+4.$

109. Body kvadratické funkce

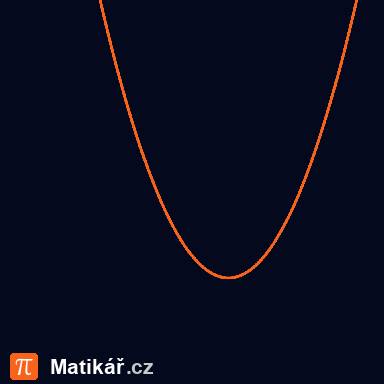
Je dána funkce g: $ y = x^2 - 4x + 3 $.

Určete všechna reálná čísla x tak, aby platilo g(x) = g(-2).

Řešení

x = –2 a x = 6

Matematická úloha – Body kvadratické funkce

110. Jízda automobilu po okruhu

Automobil projel jeden okruh neznámou stálou rychlostí, další dva stejné okruhy stálou rychlostí 72 km/hod. Celková průměrná rychlost byla 36 km/hod.

Určete v km/h rychlost, kterou automobil projel poprvé okruh.

Řešení

Automobil projel poprvé okruh rychlostí 18 km/hod.

Matematická úloha – Jízda automobilu po okruhu

111. Logaritmické rovnice

Vyřešte logaritmické rovnice:

a) $\log \left (2x + 8 \right ) = 2$

b) $\log_{6} \left (2x + 8 \right ) = 2$

c) $\log_{4} \left (2x + 8 \right ) = 2$

d) $\log_{\frac{1}{3}} \left (2x + 8 \right ) = 2$

e) $\log \left (9 - x \right ) = 2$

f) $\log_{6} \left (9 - x \right ) = 2$

g) $\log_{2} \left (9 - x \right ) = 2$

h) $\log_{\frac{1}{3}} \left (9 - x \right ) = 2$

Řešení

a) $x=46$

b) $x=14$

c) $x=4$

d) $x=-\frac{71}{18}$

e) $x=-91$

f) $x=-27$

g) $x=5$

h) $x=\frac{80}{9}$

Matematická úloha – Logaritmické rovnice

112. Graf lineární funkce

Načrtněte graf funkce

a) $y = -2x + 3$

b) $y = -\frac{1}{2}x + 1$

c) $y = \frac{1}{2}x + 1$

d) $y = \frac{3}{2}x - 1$

Řešení

Matematická úloha – Graf lineární funkce

113. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:

a) $\frac{2^{4}}{\left( 2^{2} \right )^{3}}$

b) $\frac{3^{3} \cdot 45^{3} \cdot 5^{2}}{5^{4} \cdot 3^{4}}$

c) $\frac{2^{2} \cdot \left( \frac{7}{2} \right )^{3}}{28^{3}}$

d) $\frac{2^{3} \cdot 36^{2}}{\left( \frac{4}{9} \right )^{2}}$

e) $\frac{\left( \frac{4}{25} \right )^{2} \cdot \left( 2^{2} \right )^{3}}{10^{3} \cdot 2^{2} \cdot 2^{2}}$

f) $\frac{\left( 7^{2} \right )^{4} \cdot 7^{4}}{7^{2} \cdot 14^{2} \cdot \left( \frac{7}{2} \right )^{2}}$

Řešení

a) $\frac{ 1 }{ 2^{2} }$

b) $3^{5} \cdot 5$

c) $\frac{ 1 }{ 2^{7} }$

d) $2^{3} \cdot 3^{8}$

e) $\frac{ 2^{3} }{ 5^{7} }$

f) $7^{6}$

Matematická úloha – Mocniny s přirozeným mocnitelem

114. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:

a) $\frac{\left( 2^{2} \right )^{4}}{36^{2} \cdot 2^{3}}$

b) $\frac{7^{3} \cdot \left( \frac{25}{49} \right )^{2}}{5^{3}}$

c) $\frac{\left( 5^{4} \right )^{3} \cdot 3^{2}}{5^{3} \cdot 45^{2} \cdot 5^{4}}$

d) $\frac{2^{3} \cdot \left( \frac{7}{2} \right )^{3} \cdot 7^{4} \cdot 7^{3}}{\left( 14^{3} \right )^{3} \cdot 7^{3}}$

e) $\frac{2^{3} \cdot \left( \frac{2}{7} \right )^{3} \cdot 7^{2}}{2^{3} \cdot \left( \frac{4}{49} \right )^{3} \cdot \left( \frac{7}{2} \right )^{2}}$

f) $\frac{2^{4} \cdot \left( 3^{3} \right )^{2} \cdot \left( 2^{4} \right )^{3} \cdot 3^{4} \cdot 2^{3}}{\left( 2^{3} \right )^{3}}$

Řešení

a) $\frac{ 2 }{ 3^{4} }$

b) $\frac{ 5 }{ 7 }$

c) $\frac{ 5^{3} }{ 3^{2} }$

d) $\frac{ 1 }{ 7^{2} \cdot 2^{9} }$

e) $\frac{ 7^{3} }{ 2 }$

f) $3^{10} \cdot 2^{10}$

115. Mocniny s přirozeným mocnitelem

Upravte jako mocniny prvočísel:

a) $\frac{10^{2} \cdot 2^{2}}{\left( 5^{2} \right )^{2}}$

b) $\frac{5^{4} \cdot 2^{4} \cdot 2^{4} \cdot 5^{2}}{\left( 5^{4} \right )^{2}}$

c) $\frac{14^{2} \cdot 98^{2}}{7^{3} \cdot 2^{4}}$

d) $\frac{\left( 2^{2} \right )^{4}}{36^{2} \cdot 2^{3}}$

e) $\frac{6^{2} \cdot 18^{3}}{2^{4}}$

f) $\frac{\left( 3^{2} \right )^{2}}{\left( \frac{4}{9} \right )^{2} \cdot \left( \frac{3}{2} \right )^{2} \cdot \left( 6^{3} \right )^{2}}$

Řešení

a) $\frac{ 2^{4} }{ 5^{2} }$

b) $\frac{ 2^{8} }{ 5^{2} }$

c) $7^{3}$

d) $\frac{ 2 }{ 3^{4} }$

e) $3^{8} \cdot 2$

f) $\frac{ 1 }{ 2^{8} }$

116. Algebraické výrazy

Zjednodušte výraz

\[ \frac{2x}{x-2}-\frac{7}{x+2}-\frac{x^{2}+x+10}{x^{2}-4} \]

Řešení

\[ \frac{x-2}{x+2} ; \left (x\neq \pm 2 \right ) \]

117. Body náležící kvadratické funkci

Jsou dány body A[0;-6], B[2;-4] a C[3;6]. Tyto body náleží kvadratické funkci.

Určete obecnou rovnici této kvadratické funkce.

Řešení

$ y = 3x^{2}-5x-6 $

Matematická úloha – Body náležící kvadratické funkci

118. Posloupnost Bolka a Lolka

Bolek a Lolek měli každý svou aritmetickou posloupnost. Jak Lolkova, tak Bolkova posloupnost začínala číslem 2 023 a končila číslem 3 023. Tyto dvě posloupnosti měly 26 společných čísel. Poměr Bolkovy a Lolkovy diference byl 5:2.

Vypočítejte, jaký byl rozdíl Bolkovy a Lolkovy diference.