Kamila je 2× starší než Helena. Před 4 roky byla Kamila 6× starší, než tehdy byla Helena.

Ve třídě je 30 žáků. Věk každého počítáme na celé roky. Průměrný věk dívek je 12,25 a chlapců 12,50 a průměrný věk všech je 12,30.

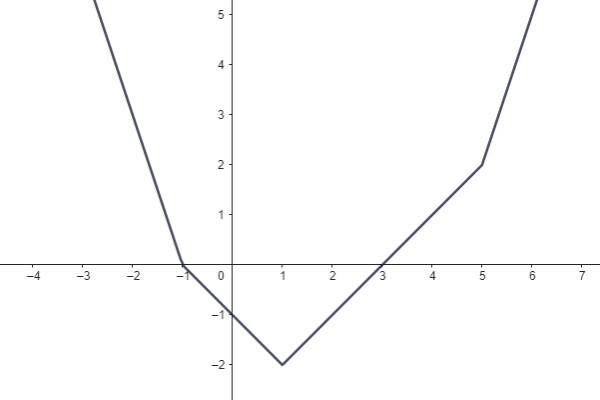
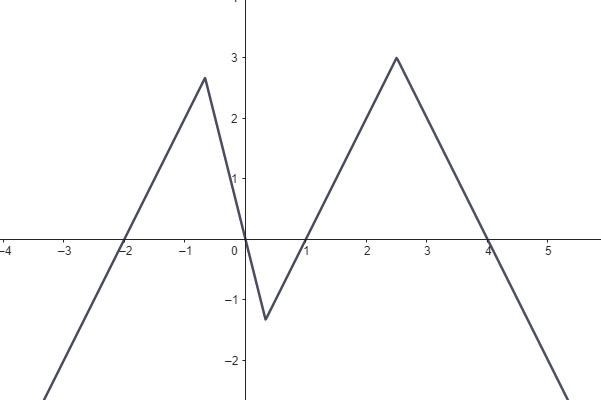
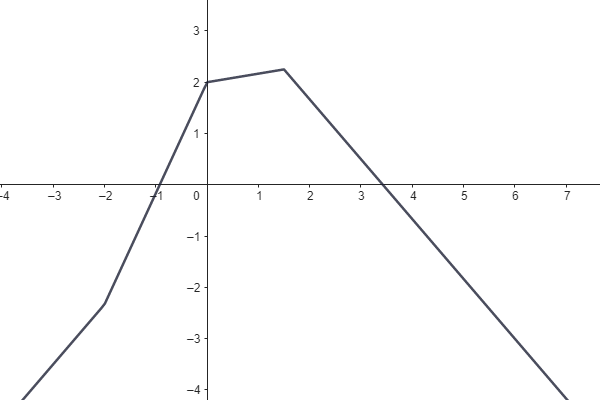
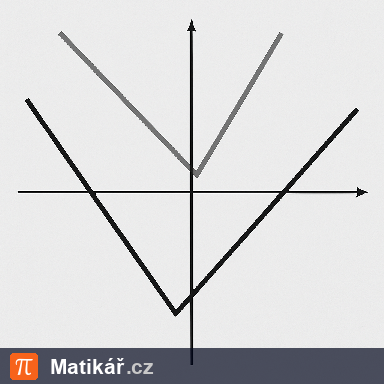
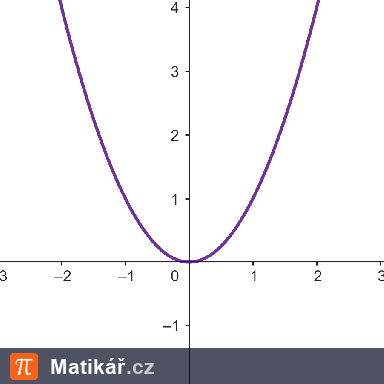
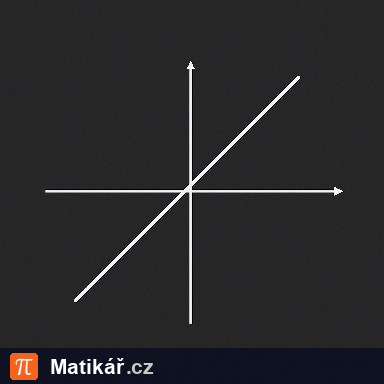
Jsou dány grafy lineárních funkcí.






V ročníku je 88 studentů a ti mají možnost si zvolit výuku dvou jazyků – angličtinu a němčinu. Na angličtinu nechodilo 66 studentů, což je o 3 více než počet studentů, kteří se nepřihlásili na němčinu. Na oba jazyky se přihlásilo 9 studentů.

Po skončení schůzky si všichni přítomní potřásli každý s každým rukou – celkem 105krát.

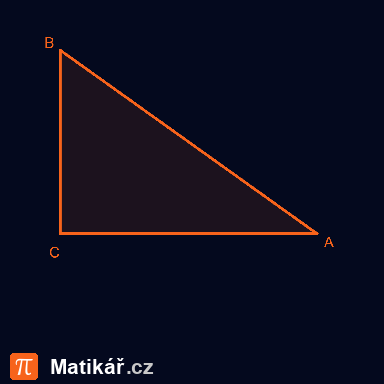
Pravoúhlý trojúhelník má obvod 36 cm. Přepona je o 6 cm delší než kratší z odvěsen.
Objem pravidelného čtyřbokého jehlanu je 288 dm³. Obvod jeho podstavy je stejně velký jako jeho výška.

Podle klinických studií je účinnost léku 90 %. Lékař lék předepsal osmi pacientům.

Délky stran pravoúhlého trojúhelníku tvoří první 3 členy aritmetické posloupnosti. Obsah trojúhelníku je 600 cm2.
Hodíme kostkou a pak hodíme tolikrát mincí, jaké číslo padlo na kostce.

Linkový autobus jezdí mezi místy A a B. Jestliže zvýší svoji průměrnou rychlost o 5 km/h, zkrátí se jízdní doba o 20 minut. Sníží-li svou původní rychlost o 4 km/h, prodlouží se doba jízdy o 20 minut.

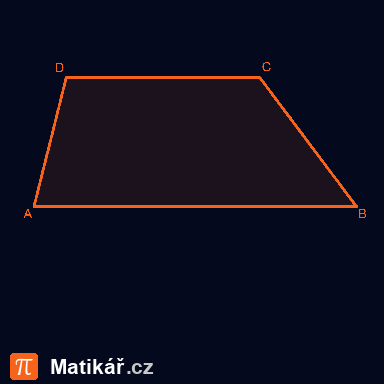
Jedna ze základen lichoběžníku je o pětinu větší než jeho výška, druhá je větší o 1 cm. Plocha lichoběžníku 115 cm2.
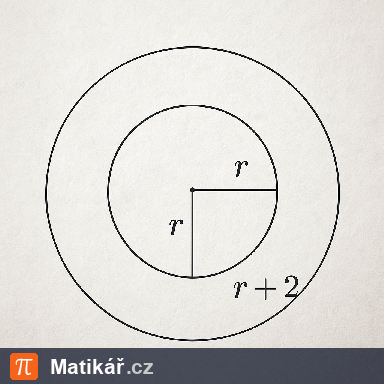
Poloměr kruhu byl zvětšen o 2 cm a tím se zvětšil jeho obsah o 40\( \pi \) cm2.
Pole má jednu stranu o polovinu delší než druhou. Plocha pole je 96 hektarů.

Cena pamětí do počítače během roku dvakrát klesla o stejné procento tak, že se
z 5 200 Kč snížila na 3 757 Kč.