Úlohy: 61–80 / 179

23456
Přehled ročníků

61. Kvadratické lomené rovnice

Vyřešte kvadratické lomené rovnice:
a)   
b)   
c)   
d)   
Řešení
a)   
b)   
c)   
d)   

62. Zapomenutý PIN

Tomáš zapomněl čtyřmístný PIN, pamatuje si první tři čísla. Ví, že čtvrté číslo je liché.

Vypočítejte pravděpodobnost v procentech, že se mu PIN podaří na jeden pokus určit.
Řešení
Pravděpodobnost, že Tomáš určí správně PIN, je 20 %.

63. Sportovní anketa

Anketa provedená u 200 respondentů zjišťovala, jaký mají rádi sport. Na výběr byl fotbal, hokej a basketbal. Přinesla tyto výsledky: Hokej je oblíben u 78 respondentů, basketbal u 75 respondentů a fotbal u 101 respondentů. Dále se zjistilo, že všechny tři sporty jsou oblíbené 28 respondenty. Těch, kteří mají rádi právě dva z těchto tří sportů, je 22, z nich právě polovina má ráda dvojici fotbal a basketbal. Respondentů, kteří mají rádi jenom basketbal, je o 7 méně než těch, kteří mají rádi jen hokej.

Vypočítejte:
a)   kolik studentů má rádo fotbal,
b)   kolik studentů má rádo hokej,
c)   kolik studentů má rádo basketbal,
d)   kolik studentů nemá rádo ani jeden z uvedených sportů.
Řešení
a)   Fotbal má rádo 101 respondentů.
b)   Hokej má rádo 78 respondentů.
c)   Basketbal má rádo 75 respondentů.
d)   24 nemá rádo ani jeden z uvedených sportů.

64. Obsah obdélníku

Obsah obdélníku je 81,25 cm2. Zvětšíme-li jeho délku o 5 mm, zvětší se jeho obsah o 4 %.

Určete v milimetrech rozměry obdélníku.
Řešení
Šířka obdélníku je 125 mm, délka obdélníku je 65 mm.

65. Šestiboký jehlan

Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm.

Vypočítejte v cm3 objem jehlanu. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Objem jehlanu je 5 196,15 cm3

66. Grafy lineárních funkcí

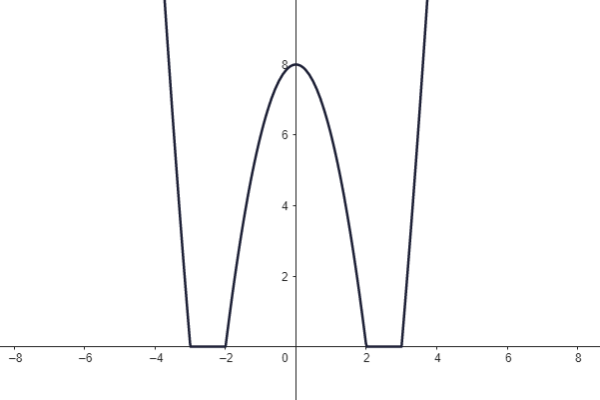
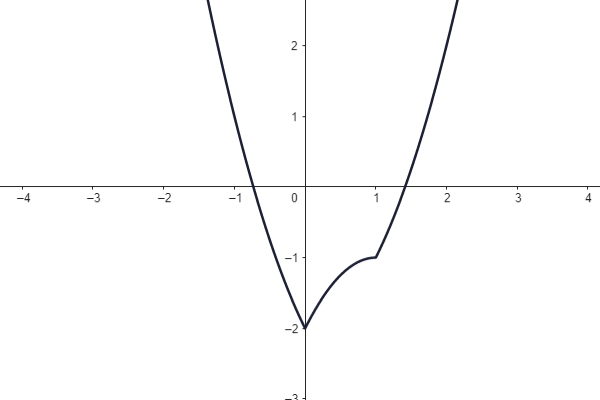
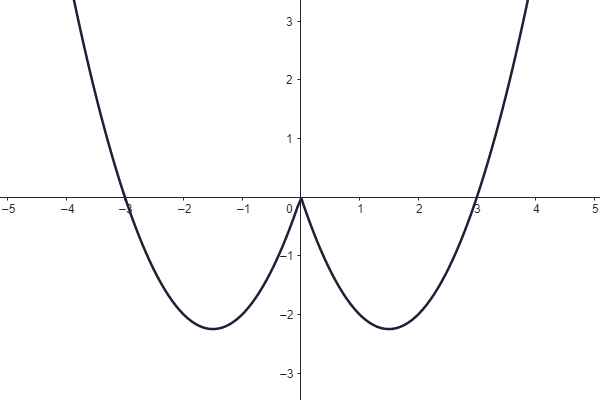
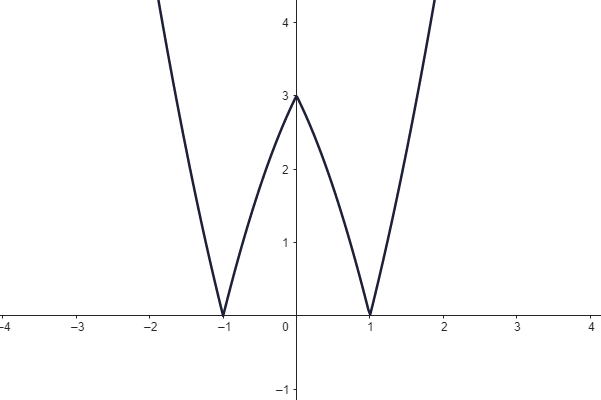
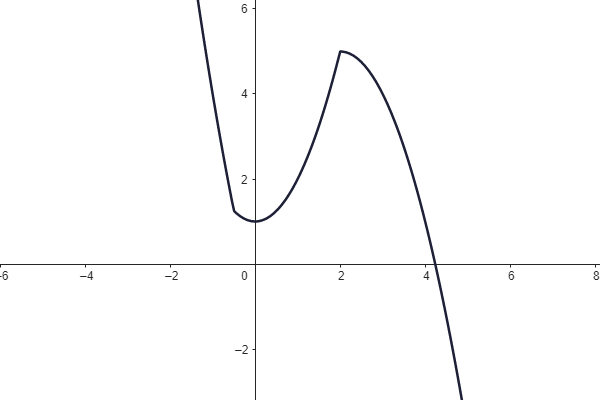
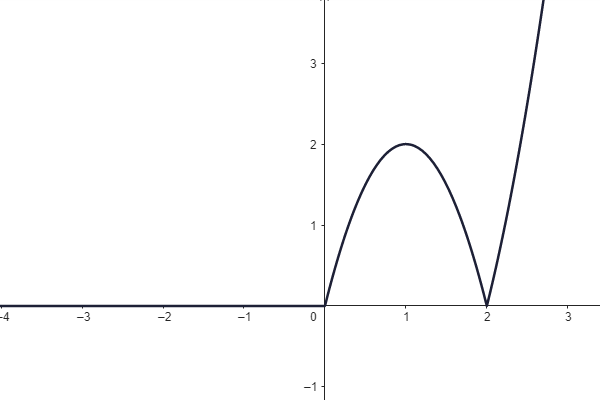
Jsou dány grafy lineárních funkcí.

Určete zpaměti funkční předpis.
a)    Graf lineární funkce
b)    Graf lineární funkce
c)    Graf lineární funkce
d)    Graf lineární funkce
Řešení
a)   
b)   
c)   
d)   

67. Opsaná a vepsaná koule

Krychli o objemu 4 096 cm3 je opsána a vepsána koule.

Vypočítejte, kolikrát je větší objem opsané koule než koule vepsané. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Objem opsané koule je 5,20krát větší než objem koule vepsané.

68. Kvadratické funkce s absolutní hodnotou

Načrtněte graf kvadratické funkce s absolutní hodnotou:
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)    Kvadratická funkce s absolutní hodnotou
b)    Kvadratická funkce s absolutní hodnotou
c)    Kvadratická funkce s absolutní hodnotou
d)    Kvadratická funkce s absolutní hodnotou
e)    Kvadratická funkce s absolutní hodnotou
f)    Kvadratická funkce s absolutní hodnotou

69. Věk dívek

Kamila je 2× starší než Helena. Před 4 roky byla Kamila 6× starší, než tehdy byla Helena.

Vypočítejte, za kolik let bude věk Kamily a Heleny v poměru 4:3.
Řešení
Věk Kamily a Heleny bude v poměru 4:3 za 10 let.

70. Žáci ve třídě

Ve třídě je 30 žáků. Věk každého počítáme na celé roky. Průměrný věk dívek je 12,25 a hochů 12,5 a průměrný věk všech je 12,3.

Vypočítejte, kolik je ve třídě dívek a kolik hochů.
Řešení
Ve třídě je 24 dívek a 6 chlapců.

71. Grafy lineárních funkcí

Jsou dány grafy lineárních funkcí.

Určete zpaměti funkční předpis.
a)    Graf lineární funkce
b)    Graf lineární funkce
c)    Graf lineární funkce
d)    Graf lineární funkce
Řešení
a)   
b)   
c)   
d)   

72. Kvadratické nerovnice

Řešte v R kvadratické nerovnice:
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
i)   
j)   
k)   
l)   

73. Počet řešení kvadratické rovnice

Určete hodnotu m tak, aby kvadratická rovnice měla jedno řešení.
a)   
b)   
c)   
d)   
Řešení
a)   m = 4
b)   m1 = -3, m2 = 3
c)   m = 3
d)   m = 0,20

74. Volba jazyků

V ročníku je 88 studentů a ti mají možnost si zvolit výuku dvou jazyků – angličtinu a němčinu. Na angličtinu nechodilo 66 studentů, což je o 3 více než počet studentů, kteří se nepřihlásili na němčinu. Na oba jazyky se přihlásilo 9 studentů.

Vypočítejte:
a)   kolik studentů se přihlásilo alespoň na jeden jazyk,
b)   kolik studentů se přihlásilo právě na jeden jazyk.
Řešení
a)   Alespoň na jeden jazyk se přihlásilo 38 studentů.
b)   Právě na jeden jazyk se přihlásilo 29 studentů.

75. Potřásání rukou

Po skončení schůzky si všichni přítomní potřásli každý s každým rukou – celkem 105krát.

Vypočítejte, kolik lidí bylo na schůzce.
Řešení
Na schůzce bylo 21 lidí.

76. Pravoúhlý trojúhelník

Pravoúhlý trojúhelník má obvod 36 cm. Přepona je o 6 cm delší než kratší z odvěsen.

Vypočítejte délky stran trojúhelníka.
Řešení
Velikost kratší z odvěsen je 9 cm, velikost delší z odvěsen je 12 cm, velikost přepony je 15 cm.

77. Pravidelný čtyřboký jehlan

Objem pravidelného čtyřbokého jehlanu je 288 dm³. Obvod jeho podstavy je stejně velký jako jeho výška.

Vypočítejte povrch jehlanu. (Výsledek zaokrouhlete na celé dm².)
Řešení
Povrch jehlanu je 326 dm².

78. Účinnost léku

Podle klinických studií je účinnost léku 90 %. Lékař lék předepsal osmi pacientům.

Vypočítejte pravděpodobnost, že u všech těchto pacientů bude lék účinný. (Zaokrouhlete na celá procenta).
Řešení
Pravděpodobnost, že u všech osmi pacientů bude lék účinný je 43 procent.

79. Pravoúhlý trojúhelník

Délky stran pravoúhlého trojúhelníku tvoří první 3 členy aritmetické posloupnosti. Obsah trojúhelníku je 600 cm2.

Určete délky stran trojúhelníku.
Řešení
Délky stran trojúhelníku podle velikosti jsou 30, 40 a 50.

80. Hod kostkou a mincí

Hodíme kostkou a pak hodíme tolikrát mincí, jaké číslo padlo na kostce.

Vypočítejte v procentech, jaká je pravděpodobnost, že padne na minci alespoň jednou hlava.
Řešení
Pravděpodobnost je 83,59 procent.
 
23456