Matikář - Úlohy na procvičení

Úlohy: 21–40 / 179

Určete determinant matice:

a) \[ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \]

b) \[ \begin{pmatrix} 2 & 0 & 1 \\ 3 & 1 & 0 \\ 4 & 1 & 2 \end{pmatrix} \]

c) \[ \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 2 & 4 & 6 \end{pmatrix} \]

d) \[ \begin{pmatrix} 3 & 1 & 2 \\ 1 & 4 & 5 \\ 6 & 2 & 1 \end{pmatrix} \]

e) \[ \begin{pmatrix} 1 & 3 & 2 \\ 0 & 1 & 4 \\ 3 & 5 & 6 \end{pmatrix} \]

f) \[ \begin{pmatrix} 1 & 0 & 2 \\ 2 & 1 & 3 \\ 3 & 2 & 4 \end{pmatrix} \]

Řešení

a) 0

b) 3

c) 0

d) -33

e) 16

f) 0

22. Průsečík dvou rovin

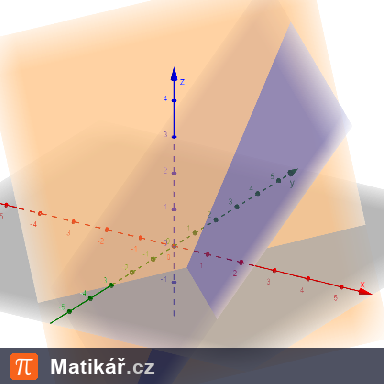
Jsou dány dvě roviny:

$ x + y - z = 0 $

$ -2x + y - z + 3 = 0 $

Určete průsečík těchto rovin.

Řešení

Průsečíkem rovin je přímka $ x + y - z = 0 $ a $ -2x + y - z + 3 = 0 $.

23. Řešení soustavy Gaussovou eliminací

Je dána soustava rovnic o 4 neznámých

\[ \begin{aligned} 3x_1 + 2x_2 - x_3 + 4x_4 &= 10 \\ x_1 - x_2 + 2x_3 - 3x_4 &= -5 \\ 4x_1 + 3x_2 + x_3 - x_4 &= 12 \\ 2x_1 + x_2 + 3x_3 + 2x_4 &= 7 \end{aligned} \]

Ověřte Frobeniovu podmínku a soustavu vyřešte pomocí Gaussovy eliminační metody.

Řešení

$ x_1 = 2 $, $ x_2 = -1 $, $ x_3 = 3 $, $ x_4 = -2 $

24. Hodnost matic 1

Určete hodnost následujících matic:

a) \[ A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \]

b) \[ B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]

c) \[ C = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \\ 3 & 6 & 9 \end{pmatrix} \]

d) \[ D = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \end{pmatrix} \]

e) \[ E = \begin{pmatrix} 0 & 2 & 4 \\ 1 & 0 & 3 \\ 5 & 6 & 0 \end{pmatrix} \]

f) \[ F = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 5 & 7 \\ 0 & 1 & 3 \end{pmatrix} \]

Řešení

a) Hodnost 2, matice je singulární.

b) Hodnost 3, matice je regulární.

c) Hodnost 1, matice je singulární.

d) Hodnost 3, matice je regulární.

e) Hodnost 3, matice je regulární.

f) Hodnost 2, matice je singulární.

25. Body na jedné přímce

Rozhodněte, zda tři body leží na jedné přímce, nebo ne.

a) A[1; 2], B[2; 4], C[3; 6]

b) A[0; 0], B[1; 3], C[2; 5]

c) A[-1; 2], B[0; 0], C[2; -4]

d) A[1; 1], B[2; 3], C[4; 5]

e) A[0; 1], B[2; 3], C[4; 5]

f) A[2; -1], B[4; 1], C[6; 3]

Řešení

a) 1

b) 0

c) 1

d) 0

e) 1

f) 0

26. Existence pravoúhlého trojúhelníku

Jsou zadané body v rovině $ A[1; 1] $, $ B[2; 4] $, $ C[7; -1] $.

Určete, jestli zadané body tvoří pravoúhlý trojúhelník.

Řešení

Body $ A[1; 1] $, $ B[2; 4] $, $ C[7; -1] $ tvoří pravoúhlý trojúhelník.

27. Exponenciální rovnice

Najděte řešení exponenciálních rovnic:

a) $3^{x-1} - 3^{x} + 3^{x+1}=567$

b) $6 \cdot 2^{x+1} - 20 \cdot 2^{x-1} =16$

Řešení

a) x = 5

b) x = 3

28. Průsečíky kvadratických funkcí

Najděte průsečíky funkcí

a) $f \left (x \right ) = x^{2} - 5x + 8, g \left (x \right ) = x^{2} - 3x - 4$

b) $f \left (x \right ) = x^{2} - 4, g \left (x \right ) = x + 2$

c) $f \left (x \right ) = x^{2} + 2x + 3, g \left (x \right ) = - x^{2} + 2$

d) $f \left (x \right ) = x^{2} + 4x + 3, g \left (x \right ) = 3 - x^{2}$

e) $f \left (x \right ) = x^{2} + 2x + 3, g \left (x \right ) = \frac{x^2}{2} + x + \frac{5}{2}$

f) $f \left (x \right ) = \left (x - 2 \right )^{2} - 1, g \left (x \right ) = \left (x - 3 \right ) \cdot \left (x - 1 \right )$

Řešení

a) $P \left [6; 14 \right ]$

b) $P_1 \left [-2; 0 \right ], P_2 \left [3; 5 \right ]$

c) nemá průsečíky

d) $P_1 \left [-2; -1 \right ], P_2 \left [0; 3 \right ]$

e) $P \left [-1; 2 \right ]$

f) nekonečně mnoho řešení $P \left [x; x^{2} - 4x + 3 \right ]$

29. Kvadratická funkce zadaná třemi body

V kartézské soustavě souřadnic jsou dány body.

Určete předpis kvadratické funkce, která prochází body:

a) $A[-2;10], B[0;2], C[1;-1]$

b) $A[-2;-10], B[1;8], C[2;18]$

c) $A[-3;-5], B[-1;-2], C[1;1]$

d) $A[0;5], B[2;-3], C[4;-19]$

e) $A[2;1], B[5;-2]$

f) $A[1;5], B[3;-13], C[5;-47]$

Řešení

a) $f \left (x \right ) = x^{2} - 4x + 2$

b) $f \left (x \right ) = x^{2} + 7x$

c) nemá řešení

d) $f \left (x \right ) = -x^{2} - 2x + 5$

e) nekonečně mnoho řešení

f) $f \left (x \right ) = -2x^{2} - x + 8$

30. Budova ve tvaru písmene H

Budova ve tvaru písmene H se skládá ze 3 částí. Dvě stejné části mají následující rozměry, výška 805 cm, šířka 525 cm, délka je 15 m. Třetí část ve tvaru krychle má šířku 7 m.

Vypočítejte, jaký je celkový objem budovy v metrech krychlových. (Zaokrouhlete na dvě desetinná místa.)

Řešení

Celkový objem budovy je 1 611,63 m³.

31. Úhlopříčky v rovnoběžníku

Je dán rovnoběžník KLMN, ve kterém známe velikosti stran $ a = |KL| = 84,5 \, \mathrm{cm} $, $ d = |KN| = 47,8 \, \mathrm{cm} $ a velikost úhlu $ \alpha = \angle NKL = 56^\circ 40' $.

Vypočítejte v centimetrech velikost

a) úhlopříčky $ e = |KM| $,

b) úhlopříčky $ f = |LN| $.

Řešení

a) Úhlopříčka e je dlouhá 99,86 cm.

b) Úhlopříčka f je dlouhá 166,52 cm.

32. Rovnice kružnice

Napište rovnici kružnice, která prochází body Q[3; 5], R[2; 6] a má střed na přímce $2x+3y-4=0$ .

Řešení

$(x + 1)^2 + (y - 2)^2 = 25$

V základní škole psali test, v němž každý žák mohl získat nejvýše 15 bodů. Letos byl průměrný bodový zisk žáků zaokrouhlený na desetiny roven 10,40. Libor si po testu uvědomil, že některé otázky si špatně přečetl a odpověděl na něco jiného. Mohl tak mít o 4 body více a průměrný bodový zisk zaokrouhlený na desetiny by se tím zvýšil na 10,60.

Vypočítejte, kolik

a) nejméně dětí mohlo psát test,

b) nejvíc dětí mohlo psát test.

Řešení

a) Minimální počet dětí, které mohly psát test, je 14.

b) Maximální počet dětí, které mohly soutěžit, je 40.

34. Trosečník na ostrově

Trosečník přišel na pustý ostrov se 4 obilnými zrnky. Z jednoho zrnka získal 10 zrnek a na chléb potřeboval 1 kg obilí a 1 zrnko má hmotnost asi 0,20 g? (Předpokládejme jednu úrodu za rok.)

Vypočítejte, kolik let trosečníkovi trvalo, než si vypěstoval dost obilí na chléb.

Řešení

Trosečníkovi trvalo 4 roky, než si vypěstoval dost obilí na chléb.

35. Třídička brambor

Kvůli velké úrodě brambor letos přikoupili na statku ke staré třídičce novou, výkonnější. Nyní pracují oba stroje současně, a proto je denní sklizeň zpracována za 12 hodin. Kdyby pracoval pouze starý stroj, potřeboval by ke zpracování denní sklizně o 10 hodin více než samotný nový stroj.

Vypočítejte, jak dlouho by to staré třídičce trvalo. Zapište v hodinách a minutách.

Řešení

Staré třídičce by to trvalo 30 hodin.

36. Násobení zlomků s neznámou

Když sečteme zlomky $\frac{10}{3}$ a $\frac{10}{x}$ dostaneme stejný výsledek, jako když je vynásobíme.

Vypočítejte hodnotu x.

Řešení

Řešením je číslo 7.

37. Tisk papíru

Tiskárna vytiskne 5 stránek za p sekund.

Vypočítejte, kolik stránek vytiskne tiskárna za p minut.

Řešení

Za p minut vytiskne tiskárna 300 stránek.

38. Ukládání knih do knihovny

Lucie má 5 různých knih, z nichž 2 určité knihy chtějí být vedle sebe na polici.

Vypočítejte, kolika různými způsoby může Lucie uspořádat všech 5 knih na polici s tímto požadavkem.

Řešení

Lucie může naskládat knihy do knihovny 48 možnými způsoby.

39. Výběr filmů

Evžen si stáhl 5 různých filmů ale má čas si pustit pouze 3, je jedno v jakém pořadí.

Vypočítejte, kolika různými způsoby může Evžen vybrat filmy, které si pustí.

Řešení

Evžen může vybrat filmy 10 různými způsoby.

40. Definiční obor funkcí 1

Určete definiční obory $ D_f $ následujících funkcí:

a) \[ f(x) = \frac{1}{x - 2} \]

b) \[ g(x) = \sqrt{5 - x} \]

c) \[ h(x) = \ln(x + 3) \]

d) \[ k(x) = \frac{\sqrt{x + 1}}{x - 4} \]

e) \[ m(x) = \sqrt{3x + 9} \]

f) \[ n(x) = \frac{\ln(x)}{x^2 - 1} \]

Řešení

a) \[ D_f = (-\infty, 2) \cup (2, \infty).\]

b) \[ D_g = (-\infty, 5\rangle.\]

c) \[ D_h = (-3, \infty).\]

d) \[ D_k = \langle -1, 4) \cup (4, \infty).\]

e) \[ D_m = \langle -3, \infty).\]

f) \[ D_n = (0, 1) \cup (1, \infty).\]

123 4 5

Střední škola

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení

Řešení