Úlohy: 1–20 / 95

12345
Přehled ročníků

1. Pozemek ve tvaru lichoběžníku

Pozemek má tvar pravoúhlého lichoběžníku se základnami 21 m a 11,20 m. Při ceně 2 500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1 352 400 korun.

Vypočítejte, kolik metrů pletiva je potřeba k oplocení tohoto pozemku.
Řešení
Pro oplocení tohoto pozemku je potřeba 100,80 metrů pletiva.

2. Úhlopříčky v rovnoběžníku

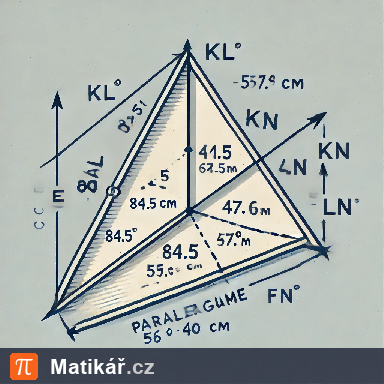
Je dán rovnoběžník KLMN, ve kterém známe velikosti stran \( a = |KL| = 84,5 \, \mathrm{cm} \), \( d = |KN| = 47,8 \, \mathrm{cm} \) a velikost úhlu \( \alpha = \angle NKL = 56^\circ 40' \).

Vypočítejte v centimetrech velikost
a)   úhlopříčky \( e = |KM| \),
b)   úhlopříčky \( f = |LN| \).
Řešení
a)   Úhlopříčka e je dlouhá 99,86 cm.
b)   Úhlopříčka f je dlouhá 166,52 cm.

3. Poměr stran obdélníku

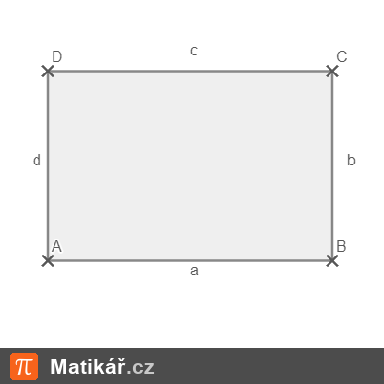
Obdélník má obvod 30 cm. Poměr délky a šířky je 2:3.

Vypočítejte:
a)   délku obdélníku v cm,
b)   šířku obdélníku v cm,
c)   obsah obdélníku v cm2.
Řešení
a)   Délka obdélníku měří 6 cm.
b)   Délka obdélníku měří 9 cm.
c)   Obsah obdélníku je 54 cm2.

4. Pletivo na výrobu klece

Klec má tvar kvádru bez spodní podstavy s rozměry 25 m, 18 m, 2,50 m.

Vypočítejte, kolik m2 pletiva je potřeba na oplocení klece.
Řešení
Celková plocha pletiva 665 m2.

5. Rozhodni o podobnosti

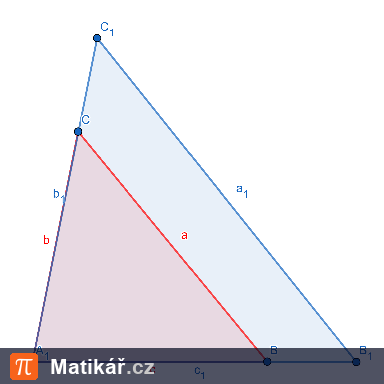
Jsou dány trojúhelníky:

∆ ABC: a = 9 m, b = 17 m, c = 12 m,

∆ DEF: d = 207 dm, e = 341 dm, f = 394 dm.

Rozhodněte, jestli jsou trojúhelníky podobné.
Řešení
a)   0
b)   1

6. Obraz s rámem

Obrazu s rámem je 92 cm široký a 57 cm vysoký. Rám má tloušťku 6 cm na všech stranách.

Vypočítejte, kolik cm2 je plocha samotného obrazu.
Řešení
Plocha obrazu je 3 600 cm2.

7. Dětský bazén

Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm.

Vypočítejte a zaokrouhlete na 2 desetinná místa:
a)   objem vody v litrech v bazénu, je-li naplněn po okraj,
b)   objem vody v litrech v bazénu, je-li naplněn po 75 % výšky,
c)   zamokřenou plochu bazénu v dm2, je-li naplněn po 75 % výšky.
Řešení
a)   Objem zcela naplněného bazénu je 6 283,19 litrů.
b)   Objem bazénu naplněného do 75 % výšky je 4 712,39 litrů.
c)   Je-li bazén naplněn po 75 % výšky, je jeho zamokřená plocha 172,79 dm2.

8. Rozloha pokoje na plánku

Rozloha pokoje čtvercového tvaru na výkresu s mírnou 1:150 je 6 cm2.

Určete skutečnou rozlohu pokoje v m2.
Řešení
Pokoj má rozlohu 13,50 m2.

9. Vystřižené rovnoramenné trojúhelníky

Jsou dány dva shodné rovnoramenné trojúhelníky, z nichž každý má obvod 100 cm. Nejprve z těchto trojúhelníků složíme rovnoběžník tak, že je k sobě přiložíme rameny. Poté z nich složíme kosočtverec tak, že je k sobě přiložíme základnami. Rovnoběžník má o 4 cm kratší obvod než kosočtverec.

Vypočítejte délky stran trojúhelníků.
Řešení
Základna má délku 32 cm, rameno má délku 34 cm.

10. Vlastnosti rovnoramenného trojúhelníku

V rovnoramenném trojúhelníku je délka ramene 25 cm, výška trojúhelníku je 24 cm.

Vypočítejte:
a)   délku základny v centimetrech,
b)   obvod trojúhelníku v centimetrech,
c)   obsah trojúhelníku v centimetrech čtverečných.
Řešení
a)   Délka základny je 14 cm.
b)   Obvod trojúhelníku je 64 cm.
c)   Obsah trojúhelníku je 168 cm².

11. Výška pravidelného čtyřbokého jehlanu

Pravidelný čtyřboký jehlan má objem 2 160 litrů a délku podstavné hrany 12 dm.

Vypočítejte výšku jehlanu.
Řešení
Výška jehlanu je 45 dm.

12. Dva čtverce

Jsou dány dva čtverce. První má délku strany 10 cm, druhý má délku strany 20 cm.

Zapište poměr:
a)   délek jejich stran,
b)   velikostí jejich obvodů,
c)   velikostí jejich obsahů.
Řešení
a)   Poměr délek stran čtverců je 1:2.
b)   Poměr obvodů čtverců je 1:2.
c)   Poměr obsahů čtverců je 1:4.

13. Objem a povrch dětského bazénu

Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm.

Vypočítejte:
a)   objem vody v litrech, který může být v bazénu, je-li naplněn po okraj (zaokrouhlete na celé litry),
b)   kolik litrů vody bude v bazénu, pokud bazén naplníme jen na do tří čtvrtin výšky (zaokrouhlete na celé litry),
c)   jak velkou plochu v m2 je třeba vymalovat, chceme-li vymalovat stěnu bazénu zevnitř beze dna (zaokrouhlete na dvě desetinná místa).
Řešení
a)   Objem vody v bazénu je 6 283 litrů.
b)   Pokud bude bazén naplněn do tří čtvrtin výšky, bude v něm 4 712 litrů vody.
c)   Je potřeba vymalovat 6,28 m2 plochy.

14. Rozdělený pravidelný čtyřboký jehlan

Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 15 cm a výškou v = 21 cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělí výšku jehlanu na tři stejné části.

Vypočítejte poměr objemů vzniklých 3 těles od nejmenšího po největší.
Řešení
Poměr je 1:7:19.

15. Cesty v parku

Cesty v parku tvoří pravoúhlý trojúhelník, jehož odvěsny mají na plánku s měřítkem 1:200 rozměry délek stran 9 cm a 12 cm. Babička chodí každý den po této trase na zdravotní procházku.

Vypočítejte
a)   kolik m2 zabírá plocha ohraničená těmito cestami,
b)   kolikrát musí babička projít všechny tři cesty, aby nachodila alespoň 1,50 km.
Řešení

16. Obcházení bazénu

Radka obešla 2× bazén. Udělala při tom 160 kroků. Když šla podél delší strany bazénu, udělala 25 kroků. Krok Radky je dlouhý 50 cm.

Vypočítejte v m2 plochu bazénu.
Řešení
Bazén zabírá plochu 93,75 m2.

17. Les na mapě

Les se čtvercovým půdorysem má rozlohu 4 km2.

Jakou stranu bude mít čtverec na mapě v měřítku 1:50 000?
Řešení
Strana čtverce na mapě bude mít délku 4 cm.

18. Obsah obdélníku

Obsah obdélníku je 81,25 cm2. Zvětšíme-li jeho délku o 5 mm, zvětší se jeho obsah o 4 %.

Určete v milimetrech rozměry obdélníku.
Řešení
Šířka obdélníku je 125 mm, délka obdélníku je 65 mm.

19. Změna strany čtverce

Čtverec má délku strany 24 cm.

Vypočítejte, jak velký bude obsah čtverce, jestliže se délka jeho strany zmenší o 25 %.
Řešení
Obsah čtverce bude 324 cm2.

20. Šestiboký jehlan

Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm.

Vypočítejte v cm3 objem jehlanu. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Objem jehlanu je 5 196,15 cm3
 
12345