Úlohy: 61–80 / 88

12345
Přehled ročníků

61. Sestrojte lichoběžník

Je dán lichoběžník ABCD (AB||CD):

|AB| = 7 cm

|BC| = 3,50 cm

|CD| = 4 cm

A velikost úhlu ABC = 60°

Proveďte náčrt, popis konstrukce a sestrojte lichoběžník ABCD.
Řešení
Matematická úloha – Sestrojte lichoběžník

62. Zvětšení kruhu

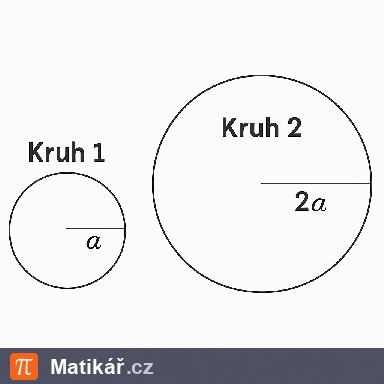
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.

Vypočtěte, kolikrát větší má kruh 2 větší než kruh 1:
a)   průměr.
b)   obvod,
c)   obsah.
Řešení
a)   Kruh 2 má 2krát větší průměr než kruh 1.
b)   Kruh 2 má 2krát větší obvod než kruh 1.
c)   Kruh 2 má 4krát větší obsah než kruh 1.
Matematická úloha – Zvětšení kruhu

63. Lesní školka

Na pozemku tvaru obdélníku stojí lesní školka. Jedna strana pozemku měří 12 m, druhá o 3 m více.

Vzájemná vzdálenost stromků je 1 m a na všech stranách 1 m od plotu.

Cena sloupku na oplocení je 200 Kč a 1 m pletiva stojí 80 Kč. Vzdálenosti mezi sloupky jsou 3 m.

Vypočtěte:
a)   kolik metrů pletiva je zapotřebí k oplocení lesní školky,
b)   kolik je ve školce stromků,
c)   kolik stojí oplocení lesní školky.
Řešení
a)   Bude zapotřebí 54 metrů pletiva.
b)   Ve školce je 130 stromků.
c)   Oplocení lesní školky stojí 7 920 Kč
Matematická úloha – Lesní školka

64. Obložení stěny

Vypočtěte, kolik čtvercových dlaždic o délce strany 10 cm je třeba na obložení stěny 2,40 m dlouhé a 1,60 m vysoké?
Řešení
Je potřeba 384 dlaždic.
Matematická úloha – Obložení stěny

65. Délka pletiva

Zahrada má tvar rovnoběžníku o rozměrech 50 m a 40 m. Stavební parcela má tvar kosočtverce, jehož strana má délku 40 m.

Vypočtěte, o kolik metrů více pletiva je potřeba k oplocení zahrady než k oplocení stavební parcely.
Řešení
Je třeba o 20 metrů více pletiva.
Matematická úloha – Délka pletiva

66. Pravidelný šestiúhelník

Je dán pravidelný šestiúhelník ABCDEF.

Určete velikost úhlu AFC.
Řešení
Velikost úhlu AFC = 60 °
Matematická úloha – Pravidelný šestiúhelník

67. Pozemek a brána

Výměra obdélníkového pozemku o délce 70 m je 2 800 m2.

Vypočtěte, kolik metrů pletiva je potřeba k oplocení pozemku, pokud vložená plechová brána má šířku 2 m?
Řešení
Je potřeba 218 m pletiva.
Matematická úloha – Pozemek a brána

68. Kružnice určené body

V rovině je 10 různých bodů.

Vypočtěte, kolik nejvíce kružnic je těmito body určeno.
Řešení
Těmito body je určeno 120 kružnic.
Matematická úloha – Kružnice určené body

69. Kuželovitá střecha

Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,30 m. Odchylka strany od roviny podstavy je 36 °.

Vypočtěte v m2 spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. (Výsledek zapište na dvě desetinná místa.)
Řešení
Spotřeba plechu je 19,40 m2
Matematická úloha – Kuželovitá střecha

70. Těžiště trojúhelníku

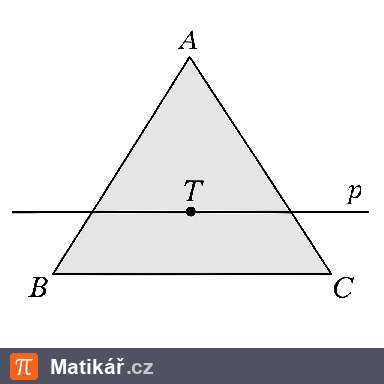
V trojúhelníku ABCE prochází přímka p těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC.

Vypočtěte poměr obsahu rozdělené menší části trojúhelníku přímkou ​​p a obsahu trojúhelníku.
Řešení
Poměr je 4:9.
Matematická úloha – Těžiště trojúhelníku

71. Úhlopříčka obrazovky

Úhlopříčka televizní obrazovky je 84 cm a výška je 40 cm.

Vypočtěte šířku obrazovky, zaokrouhlete na dvě desetinná místa.
Řešení
a = 73,86 cm
Matematická úloha – Úhlopříčka obrazovky

72. Dvě části cesty

Cesta má dvě části v celkové délce 190 metrů. Delší část cesty je o 10 metrů kratší než trojnásobek délky kratší části cesty.

Rozhodněte o každém z následujících tvrzení, zda je pravdivé, či nikoli.
a)   Delší část cesty má délku 140 metrů.
b)   Délky obou částí cesty jsou v poměru 1 : 3.
c)   Delší část cesty je o 90 metrů delší než kratší část.
Řešení
a)   1
b)   0
c)   1
Matematická úloha – Dvě části cesty

73. Kachličky v koupelně

Podlaha koupelny má tvar obdélníku o rozměrech 2 metry a 2,50 metru. Je v ní vana o rozměrech dna 150 cm a 60 cm. Zbytek podlahy je pokryt krásnými kachličkami.

Vypočtěte, na kolika metrech čtverečních jsou kachličky.
Řešení
Kachličky jsou na ploše 4,10 m2.
Matematická úloha – Kachličky v koupelně

74. Látka na sedačky

Vypočtěte, kolik m2 látky bude potřeba na potažení 12 sedaček tvaru krychle o hraně 40 cm.
Řešení
Bude potřeba 11,52 m2 látky.
Matematická úloha – Látka na sedačky

75. Kružnice a tětiva

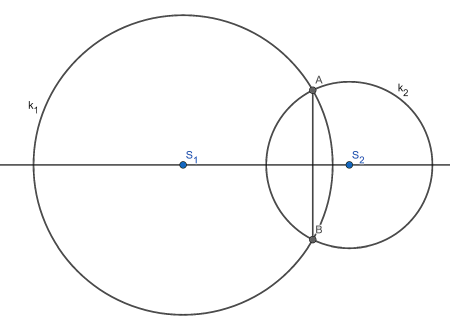
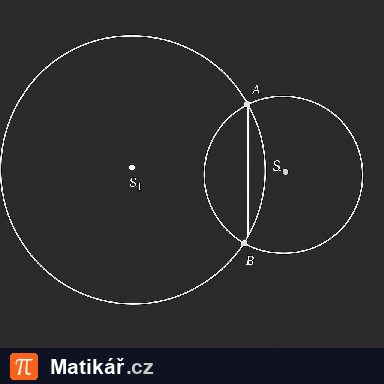
Na obrázku jsou kružnice k₁(S₁; r₁ = 9 cm) a k₂(S₂; r₂ = 5 cm). Jejich průsečíky určují společnou tětivu AB dlouhou 8 cm.

Vypočítejte v cm vzdálenost středů |S₁S₂| s přesností na dvě desetinná místa.
Dvě kružnice
Řešení
Vzdálenost středů |S₁S₂| je 11,06 cm.
Matematická úloha – Kružnice a tětiva

76. Vnitřní úhly v trojúhelníku

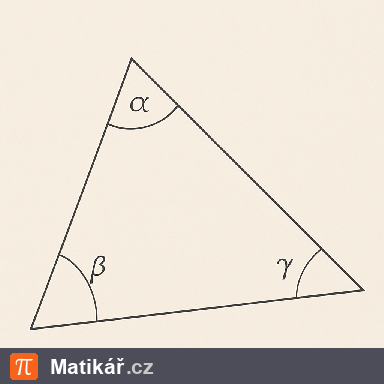
Velikosti vnitřních úhlů α, β, γ trojúhelníku jsou v poměru 3:4:5.

Vypočítejte
a)   úhel α,
b)   úhel β,
c)   úhel γ.
Řešení
a)   α = 45 °
b)   β = 60 °
c)   γ = 75 °
Matematická úloha – Vnitřní úhly v trojúhelníku

77. Objem krychlové nádoby

Nádoba tvaru krychle má bez víka povrch 320 centimetrů2.

Vypočítejte její objem v cm3.
Řešení
Objem nádoby je 512 cm3.
Matematická úloha – Objem krychlové nádoby

78. Oplocená zahrada

Karel chce oplotit svou čtvercového zahradu, strana zahrady měří 35 metrů.

Vypočtěte, jaká je celková délka plotu.
Řešení
Celková délka plotu je 140 metrů.
Matematická úloha – Oplocená zahrada

79. Obvod obdélníku

Délka obdélníku je , jeho šířka je o kratší než délka.

Vyjádřete obvod obdélníku výrazem.
Řešení
Obvod obdélníku je 2x + 20y – 12 nebo 2(x + 10y – 6).
Matematická úloha – Obvod obdélníku

80. Povrch a objem krychle

Krychle má povrch 486 dm2.

Vypočtěte v dm3 objem této krychle.
Řešení
V = 729 dm3
Matematická úloha – Povrch a objem krychle
 
12345