Graf kvadratické funkce prochází body A[1;1], B[3;-1] a C[1;2].
Na křižovatce dvou kolmých cest se rozdělila skupina turistů. Jedna skupina šla rychlostí 5,3 km/h. Druhá skupina 4,1 km/h.
Poměry stran pravoúhlého trojúhelníku jsou 3:4:5. Obvod trojúhelníka je 48 cm.


Delší rozměr obdélníkového pozemku byl zmenšen o jednu pětinu, kratší o jednu čtvrtinu.

Je dán trojúhelník ABC. Délka strany a je rovna dvou třetinám strany c. Délka strany c je rovna třem pětinám délky strany b. Délka strany b je 15 cm.
Je třeba naskládat obdélníky o rozměrech 210 mm a 84 mm tak, aby zakryly čtverec.

Příkop o průřezu tvaru rovnoramenného lichoběžníku o základnách 3 m a 5 m a ramenech o délce 2 m je hluboký 2,50 metru a dlouhý 10 metrů.

Výška věže je 56 m a vrchol věže se nachází ve výšce 55,86 m.

Ve městě se rozhodli, že postaví dětské a volejbalové hřiště. Volejbalové bude mít rozměr 12 m × 18,75 m. Dětská hřiště bude mít tvář čtverce. Plocha obou hřišť bude stejná.

Je dán trojúhelník ABC. Jeho obvod je 30 cm, přičemž strana a je o 2 cm delší než strana b a o 5 cm kratší než strana c.
Na hodinovém ciferníku navzájem spojíme body u čísel 3, 10 a 12, čímž vznikne trojúhelník.

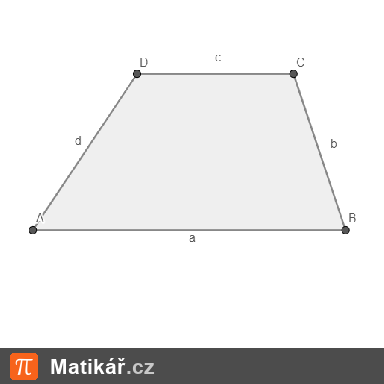
O úhlech v lichoběžníku ABCD je známo: velikost úhlu \( \gamma \) je 121 °, velikost úhlu \( \alpha \) je 2/3 úhlu \( \delta \).

Jedna strana obdélníku měří 35 cm a druhá je o 7 cm kratší než úhlopříčka obdélníku.
Je dán kvádr s rozměry 54,50 cm, 12,70 cm, 32,30 cm.
Obsah lichoběžníku je 111,80 cm2 a jeho výška 6,50 cm.
Obvod kosočtverce, který má délky úhlopříček v poměru 3:4 je 40 cm.

Pozemek, na kterém se má stavět rodinný dům, má tvar lichoběžníku se základnami o délce 42 m a 18 m, vzdálenost základen je 23 m. Dům bude mít podle projektu 146 m2 zastavěné plochy.

Hlídka měla určený pochodový úhel 13 °. Po ujetí 9 km se úhel změnil na 62 °. Tímto směrem šla hlídka 10 km.

Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.
