Adéla plánovala přečíst knihu za 6 dní. Nakonec ji ale přečetla za 5 dní, protože každý den přečetla o 4 víc, než plánovala.

Velká čokoláda stojí o třetinu více než malá čokoláda. Dvě velké a tři malé čokolády stojí 255 korun. Vedoucí koupili dětem na tábor o 10 více malých čokolád než velkých čokolád a zaplatili za ně celkem 1 710 korun.

Limonáda se prodává v malých a velkých lahvích. Malá láhev má objem 7 dl, velká 12 dl. V obchodě je velkých láhví o 10 méně než malých a celkem v nich je 469 dl limonády.

Dětský lístek do kina stál 100 korun, dospělácký stál 150 korun. V kině bylo celkem 37 návštěvníků a tržba za lístky byla 4 850 korun.

Velký sáček bonbónů stojí 25 korun, malý sáček stojí 15 korun. V regálu jsou bonbóny celkem za 1 900 korun. Malých sáčků je o 12 více než velkých.

Příkop má profil lichoběžníku. Je dlouhý 10 m, vysoký 60 cm, dno je široké 20 cm a u vršku je šířka 30 cm.

Nela, Olga a Petra mají celkem 7 500 korun. Olga má dvakrát víc než Nela. Kdyby měla Petra o 500 korun víc, měla by stejně jako Olga.

Paní učitelka koupila dětem do družiny celkem 20 hraček za 1 270 korun. Koupila autíčka po 80 korunách a panáčky po 50 kurunách.

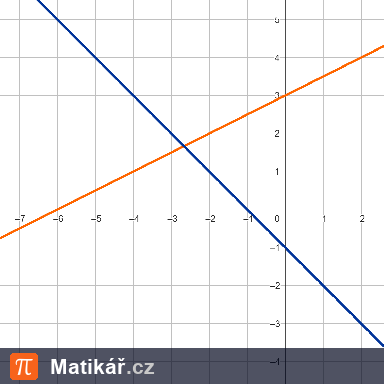
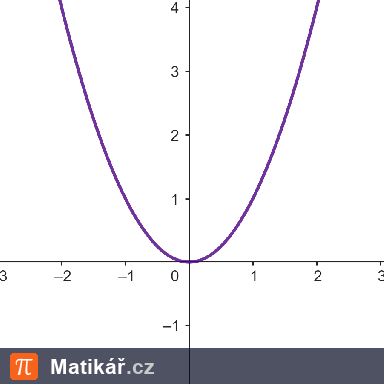
V kartézské soustavě souřadnic jsou dány body.
Bazén ve tvaru kvádru o délce 10 m, šířce 5 m a hloubce 2 m bylo potřeba vydláždit dlaždicemi o rozměru 20×20 cm. Jedna dlaždice stála 30 Kč.

Ve sklepě jsou 2litrové a 5litrové láhve s vodou. Celkem jich tam je 30, všechny jsou plné a je v nich celkem 96 litrů vody.

Malí draci jsou dvouhlaví, velcí draci jsou tříhlaví. V dračím stádu bylo 50 draků a 145 hlav.

V láhvích na polici je celkem 172 litrů vody. Do malé láhve se vejdou 2 litry, do velké 5 litrů. Všechny láhve jsou naplněné po okraj. Celkem je na polici 68 láhví.

Na letním táboře bylo 50 dětí, bydleli ve dvou a třílůžkových chatkách. Celkově děti zcela naplnily 20 chatek.

Na parkovišti stojí jen auta a autobusy. Všechna auta mají 4 kola a všechny autobusy mají šest kol. Celkem je na parkovišti 48 vozidel a dohromady mají 214 kol (rezervy nepočítáme).

Na stole leží několik velkých závaží o hmotnosti 100 g a malých závaží o hmotnosti 80 g. Závaží mají celkem hmotnost 3 800 g. Velkých je závaží je o 11 víc než malých.

50 dětí bylo na letním táboře, bydlely ve 2lůžkových a 3lůžkových pokojích. Celkem obsadily 18 pokojů. Všechny pokoje byly plně obsazeny.

Pozemek má tvar pravoúhlého lichoběžníku se základnami 21 m a 11,20 m. Při ceně 2 500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1 352 400 korun.

Budova ve tvaru písmene H se skládá ze 3 částí. Dvě stejné části mají následující rozměry, výška 805 cm, šířka 525 cm, délka je 15 m. Třetí část ve tvaru krychle má šířku 7 m.
