Do školní družiny koupili 20 sad pastelek. Větší sada stála 65 Kč, menší jen 50 Kč. Za všechny sady zaplatili 1 120 Kč.

Jolana rozdělovala bonbony. Čtvrtinu snědla, pětinu věnovala kamarádům. Zbytek bonbonů rozdělila na dvě stejné části a ty dala svým bratrům. Bratr Karel dostal 33 bonbonů.

Jana říká Haně. Teď stojí šaty 2 400 Kč. Kdyby je zlevnili o 45 %, potom o 30 % a nakonec o 25 %, byly by zadarmo.

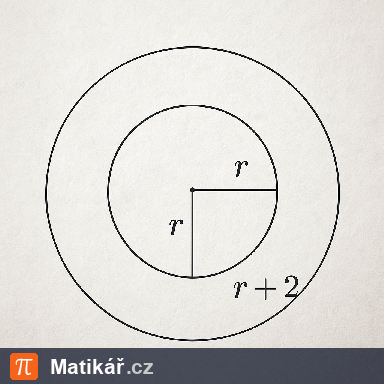
Poloměr kruhu byl zvětšen o 2 cm a tím se zvětšil jeho obsah o 40\( \pi \) cm2.
Pole má jednu stranu o polovinu delší než druhou. Plocha pole je 96 hektarů.

Cena pamětí do počítače během roku dvakrát klesla o stejné procento tak, že se
z 5 200 Kč snížila na 3 757 Kč.

První skupina turistů si koupila 8 porcí vanilkové zmrzliny a 12 porcí jahodové zmrzliny a zaplatili 360 Kč. Druhá skupina si koupila 15 porcí vanilkové zmrzliny a 10 porcí jahodové zmrzliny a zaplatila 425 Kč.

Vzdálenost z Prahy do Olomouce je 250 km. V 6 hod. vyjel z Prahy do Olomouce rychlík rychlostí 85 km/h. Ve stejném okamžiku mu vyjel naproti z Olomouce osobní vlak rychlostí 65 km/h.

Dvě letadla startující současně z letišť A a B letí navzájem proti sobě a minou se za 20 minut. Vzdálenost letišť je 220 km a průměrná rychlost letadla letícího z letiště A je o 60 km/h větší než průměrná rychlost druhého letadla.

Vzdálenost míst A a B je 132 km. V 9 hod. vyjel z místa A cyklista průměrnou rychlostí 24 km/h, v 10 hod. mu vyjel naproti z místa B druhý cyklista průměrnou rychlostí 30 km/h.

V 6 hodin 40 minut vyplul z přístavu parník rychlostí 12 km/hod. Přesně v 10 hodin za ním vyplul ze stejného místa motorový člun rychlostí 42 km/hod.

Místa A a B jsou vzdálena 23 km. Z místa A vyšel chodec průměrnou rychlostí 4 km/hod. O 45 minut později vyjel proti němu z místa B cyklista průměrnou rychlostí 16 km/hod.

Pokoj podlaha pokoje ve tvaru obdélníku má plochu 30 m2, délka je o 1 m delší než šířka. Výška pokoje je 2.5 m.

V hotelu bydlí polovina lidí v prvním patře, třetina ve druhém patře a zbylých 40 hostů v podkroví. Hotel je obsazen ze 75 %.

Tři metry první látky a čtyři metry druhé látky stojí celkem 1 420 Kč, přičemž metr druhé látky je o 110 Kč dražší než metr první látky.

Zájezd byl zdražen o šestinu a po zdražení stál 4 200 Kč.

Maminka koupila k večeři jedny sardinky a tři paštiky. Zaplatila celkem 129 Kč. Babička zaplatila za dvoje sardinky a čtyři paštiky 202 Kč.

Smísí-li se 5 kg dražšího a 10 kg levnějšího zboží, má směs cenu 220 Kč za 1 kg. Cena za jeden kilogram obou zboží se liší o 30 Kč.

Z krajského města vyjede v 9 hodin 30 minut automobil rychlostí 40 km/hod. V 11 hod. téhož dopoledne za ním vyjede motocykl rychlostí 60 km/hod.

5 krabiček slaných tyčinek a 3 láhve džusu stojí 276 korun. 3 krabičky slaných tyčinek a 2 láhve džusu stojí 176 korun.
