Na tři stromy přiletělo 36 sýkorek. Když z prvního stromu přeletělo na druhý
strom 6 sýkorek a z druhého stromu na třetí 4 sýkorky, bylo na všech stromech
stejně sýkorek.

Evžen dostal plat za brigádu. Za polovinu vydělané částky jsem si koupil kopačky a za polovinu zbytku fotbalový míč. Poté mu zbylo 1200 Kč.
Tříciferné číslo má ciferný součet 16. Pokud v tomto čísle zaměníme číslice na místech stovek a desítek, číslo se o 360 zmenší. Pokud v původním čísle zaměníme čísla na místech desítek a jednotek, číslo se o 54 zvětší.

V kontrolním testu z matematiky je 25 otázek, za každou správnou odpověď se přičte 5 bodů, za každou chybějící nebo chybně zodpovězenou otázku se odečtou 3 body. Jakub dosáhl v tomto testu 69 bodů, přičemž na dvě otázky neodpověděl.

Otec je 3× starší než syn. Za 8 let bude otec o 28 let starší než syn.

V roce 2005 byl otec třikrát tak starý než jeho syn. V roce 2020 byl syn o polovinu mladší než otec.

Tři firmy měly na účtech v bance celkem 3 250 000 Kč. První firma měla o 18 % více peněž než druhá a třetí o 47 000 Kč méně než první.

Kamarádi Martin a Jitka se rozhodli, že navštíví zámek, který je od jejich domova vzdálen 10 km. Martin vyšel v 7 hodin a 30 minut a šel rychlostí 4 km/hod. Za hodinu a půl za ním vyjela Jitka na kole a jela rychlostí 16 km/hod.

3 vejce se uvaří za 15 minut.

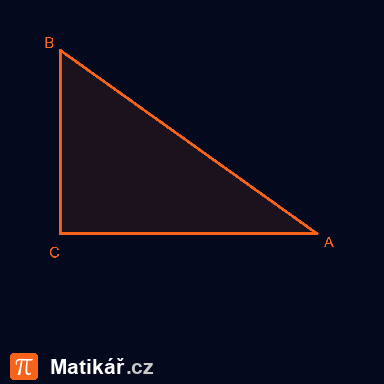
Pravoúhlý trojúhelník má obvod 36 cm. Přepona je o 6 cm delší než kratší z odvěsen.
Evžen má mince 10 Kč, 20 Kč a 50 Kč, všech je stejný počet. Dohromady má 960 Kč.

Obraz v galerii stál 300 000 Kč, ale jeho cena byla dvakrát zvýšena, pokaždé o 20 procent.

Čokoláda má na šířku 6 čtverečků, na délku má o polovinu čtverečků více.

Firma připravuje výkop na položení optického kabelu. Na výkopu pracují dva bagry, jeden by celou práci zvládl za čas o 16 hodin kratší než druhý. Společně by měly oba bagry hotovo po 15 hodinách práce.

Nádrž je možné vypustit pomocí dvou výpustí. Samotná větší výpusť vypustí nádrž za 8 hodin, samotná menší výpusť za 10 hodin. Při posledním vypouštění měly být otevřeny obě výpusti, ale závěr větší výpusti se zablokoval a povedlo se ho otevřít až hodinu po otevření menší výpusti.
Ke splnění urgentní zakázky jsou k dispozici dvě linky. Na původní lince je možné vyrobit požadované zboží za 15 hodin, na modernější ještě nespuštěné lince by mělo být zboží hotovo za 10 hodin. Původní linka může být spuštěna ihned. Novou linku je třeba ještě 4 hodiny připravovat.

Ve třídě 9. A je 29 žáků. Všichni mají být ubytováni ve 12 dvoulůžkových a třílůžkových pokojích.

Děda a jeho vnuk Honza bydlí od sebe 10 km. Domluvili se, že se sejdou na cestě mezi oběma domovy. Děda vyšel ve 13 hodin rychlostí 5 km/h. Honza mu vyjel ve stejný čas naproti na kole rychlostí 15 km/h.

Z místa A vyjel v 8 hod. kamion rychlostí 60 km/h. Z místa B, které je od A vzdálené 225 km, vyjelo ve stejnou dobu proti němu auto rychlostí 90 km/h.

Součet dvou neznámých čísel je 5× větší než jejich rozdíl. První číslo je o 5 větší než druhé.
