Matikář - kategorie úloh

Úlohy: 1–20 / 105

1. Myšlené číslo

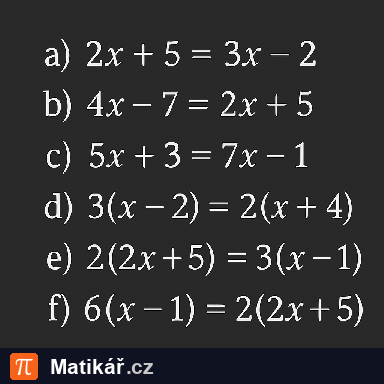
Myslím si číslo. Když od něj odečtu jeho jednu třetinu, výsledek vynásobím osmi, získaný součin vydělím třemi a číslo, které mi vyšlo, odečtu od osmi, dostanu číslo čtyři.

Vypočítejte, jaké bylo původní číslo.

Řešení

Hledané číslo je 2.25 .

2. Goniometrické rovnice 2

Vyřešte goniometrické rovnice:

a) \[ \sin x = \frac{1}{2} \]

b) \[ \cos x = -\frac{\sqrt{3}}{2} \]

c) \[ \tan x = 1 \]

d) \[ \sin 2x = 0 \]

e) \[ 2\cos^2 x - 1 = 0 \]

f) \[ \sin^2 x = \frac{1}{4} \]

Řešení

a) \[ x = \frac{\pi}{6} + 2k\pi, \, x = \frac{5\pi}{6} + 2k\pi \]

b) \[ x = \frac{5\pi}{6} + 2k\pi, \, x = \frac{7\pi}{6} + 2k\pi \]

c) \[ x = \frac{\pi}{4} + k\pi \]

d) \[ x = \frac{k\pi}{2} \]

e) \[ x = \frac{\pi}{4} + 2k\pi, \, x = \frac{3\pi}{4} + 2k\pi, \,\]\[x = \frac{5\pi}{4} + 2k\pi, \, x = \frac{7\pi}{4} + 2k\pi \]

f) \[ x = \frac{\pi}{6} + 2k\pi, \, x = \frac{5\pi}{6} + 2k\pi, \,\]\[x = \frac{7\pi}{6} + 2k\pi, \, x = \frac{11\pi}{6} + 2k\pi \]

Matematická úloha – Goniometrické rovnice 2

3. Lineární rovnice 2

Vyřešte lineární rovnice:

a) \[ \frac{x}{3} + \frac{2x}{6} = 5 + 2x \]

b) \[ \frac{3x}{4} - \frac{x}{2} = x + 1 \]

c) \[ \frac{2x}{5} + 3 = \frac{4x}{10} + 6 \]

d) \[ \frac{5x}{6} + 2 = \frac{x}{3} + 4 \]

e) \[ \frac{3x}{8} - \frac{x}{4} = \frac{5}{2} - x \]

f) \[ \frac{x}{2} + 1 = \frac{x}{4} + 2 \]

Řešení

a) \[ x = -\frac{15}{4} \]

b) \[ x = -\frac{4}{3} \]

c) \[ \text{Rovnice nemá řešení.} \]

d) \[ x = 4 \]

e) \[ x = \frac{20}{9} \]

f) \[ x = 4 \]

4. Goniometrické rovnice 1

Vyřešte goniometrické rovnice:

a) \[\sin x = \frac{1}{2}\]

b) \[\cos x = -\frac{\sqrt{2}}{2}\]

c) \[\tan x = \sqrt{3}\]

d) \[\sin^2 x = \frac{3}{4}\]

e) \[\cos 2x = 0\]

f) \[\tan^2 x = 3\]

Řešení

a) \[x = \frac{\pi}{6} + 2k\pi \lor x = \frac{5\pi}{6} + 2k\pi, k \in \mathbb{Z}\]

b) \[x = \frac{3\pi}{4} + 2k\pi \lor x = \frac{5\pi}{4} + 2k\pi, k \in \mathbb{Z}\]

c) \[x = \frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]

d) \[x = \frac{\pi}{3} + 2k\pi \lor x = \frac{2\pi}{3} + 2k\pi \lor x = \frac{4\pi}{3} + 2k\pi \lor x = \frac{5\pi}{3} + 2k\pi, k \in \mathbb{Z}\]

e) \[x = \frac{\pi}{4} + \frac{k\pi}{2}, k \in \mathbb{Z}\]

f) \[x = \frac{\pi}{3} + k\pi \lor x = -\frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]

Matematická úloha – Goniometrické rovnice 1

5. Logaritmické rovnice

Vyřešte v R logaritmické rovnice:

a) $ \log_3\left(5 + \log_2((x-1)^4)\right) = 2 $

b) $ \log_2(x) + \log_2(x - 1) = 3 $

c) $ \log_3(x^2 + 3x) - \log_3(x) = 1 $

d) $ \log_5(x^2 - 4) + \log_5(2x) = 2 $

e) $ \ln(x^2 + 2x) - \ln(x + 1) = \ln(4) $

f) $ \log_{10}(x^2 + 4x + 4) + \log_{10}(x + 3) = 2 $

Řešení

a) $ x = 3 \quad \text{a} \quad x = -1 $

b) $ x = 4 $

c) $ \text{Žádné řešení.} $

d) $ x = 3 $

e) $ x = 2 $

f) $ x = 2 $

Matematická úloha – Logaritmické rovnice

6. Logaritmické rovnice

Vyřeš logaritmické rovnice:

a) $ \log_2(x+1) + \log_2(x-1) = 3 $

b) $ \log_2(2x+3) - \log_2(x-1) = 1 $

c) $ \log_2(x+4) + \log_2(x-2) = 3 $

d) $ \log_2(x+4) + \log_2(x-2) = 3 $

e) $ \log_2(4x+1) - \log_2(x-1) = 3 $

f) $ \log(99x+100) - \log(x-1) = 2 $

Řešení

a) \[ x = 3 \]

b) \[ \text{nemá řešení} \]

c) \[ x = \frac{1 + \sqrt{41}}{2} \]

d) \[ x = -1 + \sqrt{17} \]

e) \[ x = \frac{9}{4} \]

f) \[ x = 200 \]

7. Lineární rovnice

Vyřešte rovnice a proveďte zkoušku:

a) $ (x - 5)(x + 2) = (x - 3)(x + 4) $

b) $ (x + 6)(x - 7) = (x + 4)(x - 5) $

c) $ (2x + 3)(3x - 1) = (x + 1)(6x - 2) $

d) $ (2x+2)(2x-3)=(4x+3)(x-1) $

Řešení

a) $ x = \frac{1}{2} $

b) nemá řešení

c) $ x = \frac{1}{3} $

d) $ x = -3 $

8. Lineární rovnice

Vyřešte lineární rovnice

a) \[ \frac{2x + 6}{4} = 3 \]

b) \[ \frac{3x - 9}{6} = x - 2 \]

c) \[ \frac{x + 5}{2} + \frac{x - 3}{4} = 3 \]

d) \[ \frac{4x + 8}{6} = \frac{2x}{3} + 2\]

e) \[ \frac{3x - 9}{4} = \frac{x + 3}{2}\]

f) \[ \frac{5x + 15}{8} = \frac{3x}{4} + 1\]

Řešení

a) $ x = 3 $

b) $ x = 1 $

c) $ x = 5 $

d) nemá řešení

e) $ x = 15 $

f) $ x = 7 $

9. Lineární rovnice

Vyřešte lineární rovnice a proveďte zkoušku:

a) $ 2(x + 3) = 16 $

b) $ 5(x - 2) + 3 = 3x + 9 $

c) $ 4(x + 1) = 2(x + 7) $

d) $ 3(x - 5) - 2 = x - 4 $

e) $ 6(x + 2) = 6x + 15 $

f) $ 3(x + 4) - 2x = 6 $

Řešení

a) $ x = 5 $

b) $ x = 8 $

c) $ x = 5 $

d) $ x = 6.5 $

e) nemá řešení

f) $ x = -6 $

10. Logaritmické rovnice

Vyřešte logaritmické rovnice:

a) $ \log_3 (x + 2) = 2 $

b) $ \log_5 (2x - 1) = 3 $

c) $ \log_2 (3x + 4) = 4 $

d) $ \log_4 (5x - 3) = 2 $

e) $ \log_7 (x^2 - 1) = 1 $

f) $ \log_6 (2x + 5) = 0 $

g) $ \log_9 (4x - 7) = 2 $

h) $ \log_{10} (x + 9) = 1 $

Řešení

a) $ x = 7 $

b) $ x = 63 $

c) $ x = 4 $

d) $ x = 3.8 $

e) $ x = 2\sqrt{2} $ nebo $ x = -2\sqrt{2} $

f) $ x = -2 $

g) $ x = 22 $

h) $ x = 1 $

11. Exponenciální rovnice počítané substitucí

Vypočítej exponenciální rovnice v oboru reálných čísel:

a) $ 2^{2x} - 3 \cdot 2^x + 2 = 0 $

b) $ 3^{2x} + 2 \cdot 3^x - 8 = 0 $

c) $ 5^{2x} - 6 \cdot 5^x + 5 = 0 $

d) $ 4^{2x} - 8 \cdot 4^x + 16 = 0 $

e) $ 9^{2x} - 7 \cdot 9^x + 12 = 0 $

f) $ 7^{2x} - 13 \cdot 7^x + 42 = 0 $

g) $ 6^{2x} - 5 \cdot 6^x - 6 = 0 $

h) $ 10^{2x} + 3 \cdot 10^x - 4 = 0 $

Řešení

a) $ x = 0 $ nebo $ x = 1 $

b) $ x = \log_3 2 $

c) $ x = 1 $ nebo $ x = 0 $

d) $ x = 1 $

e) $ x = \frac{1}{2} $ nebo $ x = \log_9 4 $

f) $ x = \log_7 6 $ nebo $ x = 1 $

g) $ x = 1 $

h) $ x = 0 $

Matematická úloha – Exponenciální rovnice počítané substitucí

12. Peníze tří dívek

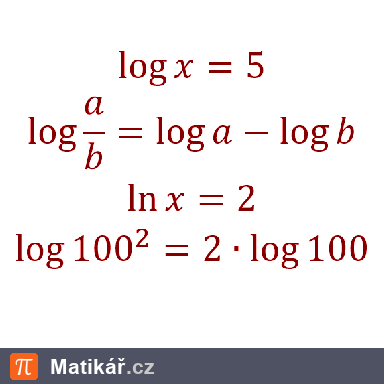
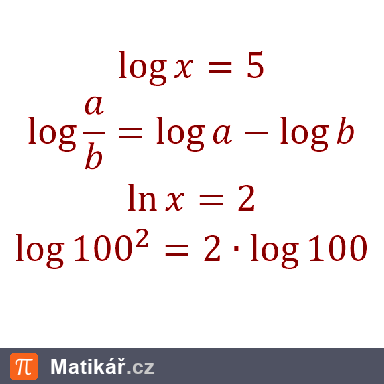
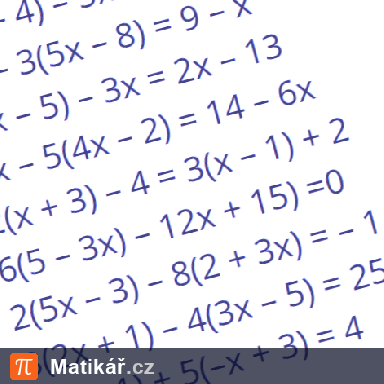
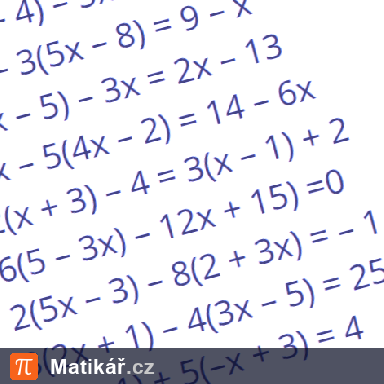
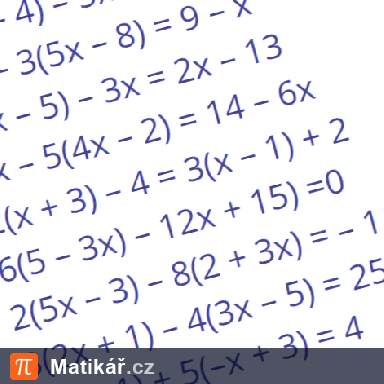
Nela, Olga a Petra mají celkem 7 500 korun. Olga má dvakrát víc než Nela. Kdyby měla Petra o 500 korun víc, měla by stejně jako Olga.

Vypočítejte, kolik korun má:

a) Nela,

b) Olga,

c) Petra.

Řešení

a) Nela má 1600 korun,

b) Olga má 3200 korun,

c) Petra má 2700 korun.

13. Jahodové a smetanové nanuky

V prodejně měli jen jahodové a smetanové nanuky. Jahodových nanuků bylo v prodejně o třetinu více než smetanových nanuků. Celkem měli v prodejně 420 nanuků.

Určete, kolik bylo v prodejně:

a) jahodových nanuků,

b) smetanových nanuků.