Pozemek, na kterém se má stavět rodinný dům, má tvar lichoběžníku se základnami o délce 42 m a 18 m, vzdálenost základen je 23 m. Dům bude mít podle projektu 146 m2 zastavěné plochy.

Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.

Vodní nádrž má tvar válce s průměrem podstavy 3 metry a hloubkou 60 cm. Voda v nádrži dosahuje do 60 % výšky nádrže.

V neprůhledném balíčku je 5 citronových, 6 jablečných a 3 jahodové bonbóny.

Z rozhledny, která je 15 m vysoká a od řeky vzdálená 30 m, vidíme řeku pod výškovým úhlem 15 °.

Střecha věže má tvar pravidelného čtyřbokého jehlanu a výškou 4 m a hranou podstavy 6 m. Zjistilo se, že je poškozeno 25 % krytiny na střeše.

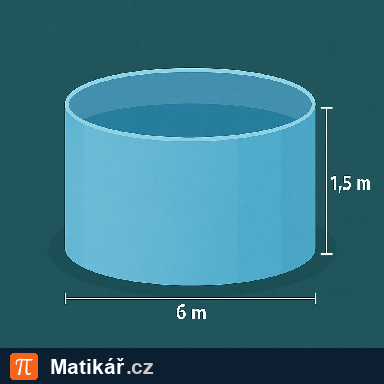
Zahradní bazén má tvar válce o průměru dna 6 m a výšce 1,50 m. Před prvním napuštěním byl natřen ochrannou barvou.
Je dán lichoběžník ABCD (AB||CD):
|AB| = 7 cm
|BC| = 3,50 cm
|CD| = 4 cm
A velikost úhlu ABC = 60°




Krabice má výšku 55 cm a šířku 40 cm. Objem krabice je 180 litrů.

Do kolekce jsou smíchány dva druhy bonbónů. Kilogram prvního druhu stojí 360 Kč, kilogram druhého druhu stojí 540 Kč. Oba druhy jsou ve směsi zastoupeny v poměru 4:6.

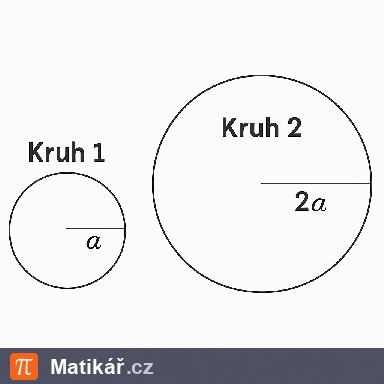
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.
Je dán pravidelný čtyřbokého jehlanu. Výška jehlanu je 30 cm a stěnová výška je 50 cm.

Je potřeba převézt zlaté cihly o rozměrech 20 × 15 × 8 cm autem, které má nosnost 3,5 t.
Hustota zlata je 19,3 .

V železářství prodávali 1 kg hřebíků za 400 Kč a 1 kg vrutů za 800 Kč. Celkem prodali 5 kg a utržili 3 200 Kč.

Patrik, Pavel, Alena a Renata šli do divadla.
V divadle je 60 % dospělých a zbytek dětí. Z dospělých je žen a 18 mužů.

Zahradnice měly zasadit 200 sazenic. Lenka zasadila o 20 % více než Dana. Eva zasadila o 40 více než Dana. Zuzka zasadila toho co Dana.

Olga jela na projížďku na kole. Za hodinu se za ní po stejné trase vypravil bratr na motorce stálou rychlostí 60 km/h a dojel ji za hodiny.
