Zedník s učedníkem by společně postavili zeď za 15 hodin. Učedník sám by zeď postavil za 60 hodin.

První čerpadlo naplní samostatně bazén za 7 hodin, druhé za 5 hodin.



Úhlopříčka televizní obrazovky je 84 cm a výška je 40 cm.

Kamarádi Petr a Martin bydlí ve vzdálenosti 13 kilometrů od sebe. Petr jel za Martinem na kole průměrnou rychlostí 18 km/hod. a Martin mu ve stejném okamžiku vyjel naproti na koloběžce. Za půl hodiny po vyjetí se setkali.

V penálu je 5 pastelek: modrá, žlutá, zelená, červená a fialová.

Z měst A a B, která jsou od sebe vzdálena 50 km, vyrazila proti sobě ve stejném čase dvě auta průměrnými rychlostmi 80 km/h (z měta A) a 120 km/h (z města B).

Čísla A a B se liší o 95. Pokud od čísla A odečteme jeho dvě třetiny, dostaneme stejný výsledek, jako když k číslu B přičteme jeho tři pětiny.


V kocourkovském hradním muzeu byl nalezen větší počet středověkých kanónů vyrobených z děloviny (dělovina je slitina cínu a mědi v poměru 1:9). Kocourkovští radní se dohodli, že kanóny nepotřebují, ale hodil by se jim nový zvon do kocourkovské věže. Zvony se vyrábějí ze zvonoviny, která je také slitinou cínu a mědi, ale v poměru 1:4.

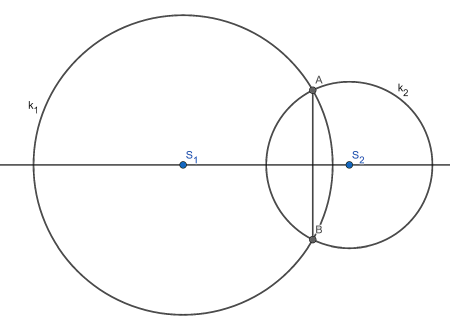
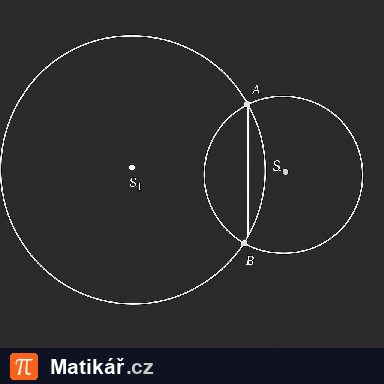
Na obrázku jsou kružnice k₁(S₁; r₁ = 9 cm) a k₂(S₂; r₂ = 5 cm). Jejich průsečíky určují společnou tětivu AB dlouhou 8 cm.
Jana, Martina a Zuzka si rozdělily bonbóny v poměru 3:7:5 . Martina dostala o 9 bonbonů méně než měly Jana a Zuzka spolu.

Máme 2 stejné modré kuličky a 2 stejné červené kuličky. Uspořádáme je všemi způsoby do řady.

Máme 6 kuliček různých barev. Najednou vybereme dvě kuličky.





Karel má v pokladničce celkem 19 mincí, a to pouze desetikorunové a padesátikorunové mince. Celkem má v pokladničce naspořeno 830 Kč.
