Úlohy: 221–240 / 247

910111213
Přehled ročníků

221. Vnitřní úhly v trojúhelníku

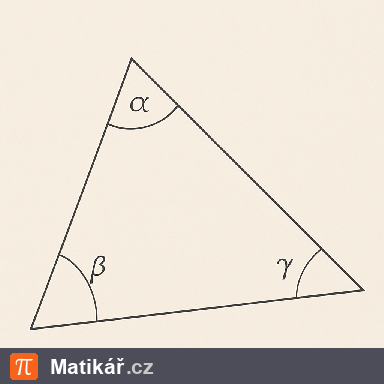
Velikosti vnitřních úhlů α, β, γ trojúhelníku jsou v poměru 3:4:5.

Vypočítejte
a)   úhel α,
b)   úhel β,
c)   úhel γ.
Řešení
a)   α = 45 °
b)   β = 60 °
c)   γ = 75 °
Matematická úloha – Vnitřní úhly v trojúhelníku

222. Ninini sourozenci

Nina má dva malé sourozence, čtyřicetiměsíční Aničku a sedmiměsíčního Káju.

Vypočtěte,
a)   za kolik měsíců bude Anička čtyřikrát starší než Kája,
b)   věkový rozdíl mezi Ninou a Aničkou, pokud Nina před čtyřmi měsíci slavila šesté narozeniny. Výsledek uveďte v měsících.
Řešení
a)   Anička bude 4krát starší za 4 měsíce.
b)   Terezka je starší o 36 měsíců.
Matematická úloha – Ninini sourozenci

223. Lepenkové krabice

Uzavřená krabice má tvar kolmého hranolu s podstavou rovnostranného trojúhelníku. Hrana podstavy je 24 cm dlouhá, výška krabice je 0,50 m.

Vypočítejte, kolik metrů čtverečních lepenky je třeba na zhotovení 20 takových krabic. (Výsledek zapište zaokrouhlený na 2 desetinná místa.)
Řešení
S = 8,20 m2
Matematická úloha – Lepenkové krabice

224. Uskladněné brambory

Firma má dva sklady brambor. V prvním skladu je třikrát více brambor než ve druhém. Z prvního skladu byla odvezena polovina zde uskladněného množství brambor a zbylo v něm o 90 tun brambor více než ve druhém skladu.

Vypočtěte,
a)   kolik tun brambor má firma uskladněno v druhém skladu brambor,
b)   kolik tun brambor bylo odvezeno z prvního skladu.
Řešení
a)   Ve druhém skladu je 180 tun brambor.
b)   Z prvního skladu bylo odvezeno 270 tun brambor.
Matematická úloha – Uskladněné brambory

225. Kamarádky na cvičení

Kamarádky Pavla, Petra a Sára si šly zacvičit. Celkem cvičily 360 minut. Pavla cvičila trojnásobek času oproti každé ze svých dvou kamarádek. Petra a Sára cvičily stejný čas.

a)   Určete, v jakém poměru jsou časy cvičení všech tří kamarádek v pořadí Pavla, Petra a Sára.
b)   Vypočtěte, kolik minut cvičila Pavla.
Řešení
a)   Poměr časů je 3:1:1.
b)   Pavla cvičila 216 minut.
Matematická úloha – Kamarádky na cvičení

226. Práce v dílnách

4 dělníci vyrobí za 8 dní 960 výrobků.

Vypočtěte, kolik dělníků vyrobí za 9 dní 2 430 výrobků.
Řešení
Je to 9 dělníků.
Matematická úloha – Práce v dílnách

227. Výroba součástek

Denní normovaný výkon pracovníka předpokládá vyrobení 530 součástek stejného druhu. Skutečný výkon pracovníka byl 702 součástek.

Vypočtěte, na kolik procent pracovník splnil plán.
Řešení
Pracovník splnil plán na 135 %.
Matematická úloha – Výroba součástek

228. Získaný úrok

Vypočítejte, za kolik let vynese jistina 50 000 Kč při 5 % p. a. úrok 5 125 Kč.
Řešení
Počet let je 2.
Matematická úloha – Získaný úrok

229. Obvod obdélníku

Délka obdélníku je , jeho šířka je o kratší než délka.

Vyjádřete obvod obdélníku výrazem.
Řešení
Obvod obdélníku je 2x + 20y – 12 nebo 2(x + 10y – 6).
Matematická úloha – Obvod obdélníku

230. Přeprava autobusy

První den bylo třeba přepravit 240 lidí, dvěma autobusy trvala přeprava 30 minut.

Vypočtěte, kolik minut trvala přeprava druhý den, jestliže bylo třeba přepravit 660 lidí a byly nasazeny tři autobusy?
Řešení
Přeprava trvala 55 minut.
Matematická úloha – Přeprava autobusy

231. Prodej kaprů

Pan Ryba za nákup tří vánočních kaprů zaplatil 1 080 Kč.

Druhý kapr bylo o 80 dkg těžší než první kapr a třetí kapry byl o 80 dkg těžší než druhý kapr. Cena za 1 kg živého kapra byla 120 Kč.

Vypočtěte v kilogramech
a)   hmotnost všech tří kaprů dohromady,
b)   hmotnost prvního kapra.
Řešení
a)   Všichni kapři měli hmotnost 9 kg.
b)   První kapr měl hmotnost 2,20 kg.
Matematická úloha – Prodej kaprů

232. Směs bonbónů

Kilogram jahodových bonbónů stojí 160 Kč, kilogram malinových bonbónů stojí 200 Kč/kg. Cukrář má připravit 20 kg směsi v ceně 190 Kč/kg. Cena směsi se stanovuje podle poměru, v jakém se bonbóny míchají.

Vypočtěte:
a)   kolik kilogramů malinových bonbónů bude ve směsi.
b)   cenu jednoho kilogramu takto namíchané směsi, pokud malinové bonbóny zdraží o 20 Kč/kg.
Řešení
a)   Ve směsi bude 15 kg malinových bonbónů.
b)   Cena směsi bude 205 Kč/kg.
Matematická úloha – Směs bonbónů

233. Rozdělení zahrady

Obsah zahrady byl rozdělen na bylinkovou, zeleninovou a okrasnou část v poměru 2 : 3 : 5 (v tomto pořadí). Výměra bylinkové části je 4 m × 2,50 m.

Vypočtěte,
a)   kolik m2 je celková rozloha zahrady,
b)   kolik procent z celkové rozlohy zahrady tvoří zeleninová část.
Řešení
a)   Celková rozloha zahrady je 50 m2
b)   Zeleninová část tvoří 30 % plochy zahrady.
Matematická úloha – Rozdělení zahrady

234. Objednávka s dopravou

Cena jednoho kusu zboží činí 350 Kč a cena dopravy je 90 Kč. Cena objednávky byla celkem 5 340 Kč.

Vypočtěte, kolik kusů zboží bylo v objednávce.
Řešení
V objednávce bylo celkem 15 kusů zboží.
Matematická úloha – Objednávka s dopravou

235. Trojciferná čísla

Jsou dány číslice 0, 1, 4 a 9.

Vypočtěte, kolik je:
a)   trojciferných čísel, pokud se číslice mohou opakovat,
b)   trojciferných čísel, pokud se číslice nemohou opakovat.
Řešení
a)   48 trojciferných čísel,
b)   18 trojciferných čísel.
Matematická úloha – Trojciferná čísla

236. Trojciferná čísla

Jsou dány číslice 1, 5, 7 a 2.

Vypočtěte,
a)   kolik je trojciferných čísel, pokud se číslice mohou opakovat,
b)   kolik je trojciferných čísel, pokud se číslice nemohou opakovat,
c)   kolik je sudých trojciferných čísel pokud se číslice mohou opakovat,
d)   kolik je lichých trojciferných čísel pokud se číslice mohou opakovat.
Řešení
a)   Trojciferných čísel je 64.
b)   Trojciferných čísel je 24.
c)   Sudých trojciferných čísel je 16.
d)   Lichých trojciferných čísel je 48.
Matematická úloha – Trojciferná čísla

237. Hustota asfaltu

Sud naplněný asfaltem má průměr 60 cm a výšku 100 cm. Hmotnost asfaltu v něm je 390 kg.

Vypočtěte hustotu asfaltu v .
Řešení
Hustota asfaltu je 1 379,86 kg/m3.
Matematická úloha – Hustota asfaltu

238. Loďka v řece

Loďka se pohybuje po proudu řeky rychlostí v1= 5 a proti proudu v2= 2 .

Vypočtěte rychlost proudu řeky a rychlost loďky vzhledem k vodě.
Řešení
a)   Rychlost proudu řeky je 1,50 km/h
b)   rychlost loďky vzhledem k vodě 3,50 km/h.
Matematická úloha – Loďka v řece

239. Bakterie ve zkumavce

Bakterie ve zkumavce se dělí každou sekundu na dvě, přičemž každá nová má stejný objem jako původní. Přesně o půlnoci byla zkumavka plná.

Vypočítejte, kolik sekund před půlnocí byla zkumavka zaplněna do poloviny.
Řešení
Počet sekund před půlnocí, kdy byla zkumavka zaplněná do poloviny, bylo 1.
Matematická úloha – Bakterie ve zkumavce

240. Dva brigádníci

Dva brigádníci očešou jablka z 15 jabloní za 5 hodin 20 minut. Po dvou hodinách práce jim přišli pomoci další tři brigádníci.

Vypočtěte, za jak dlouho celkem byla očesána jablka z těchto 15 stromů.
Řešení
Jablka ze stromů byla očesána za 3 hodiny a 20 minut.
Matematická úloha – Dva brigádníci
 
910111213