
Do kolekce jsou smíchány dva druhy bonbónů. Kilogram prvního druhu stojí 360 Kč, kilogram druhého druhu stojí 540 Kč. Oba druhy jsou ve směsi zastoupeny v poměru 4:6.

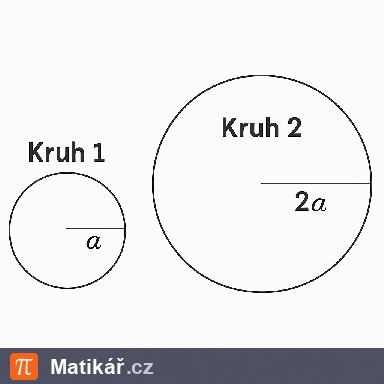
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.
Zvuk se šíří rychlostí 1 km za 3 sekundy. Hrom bylo slyšet 12 sekund po blesku.

V divadle je 60 % dospělých a zbytek dětí. Z dospělých je žen a 18 mužů.

Zahradnice měly zasadit 200 sazenic. Lenka zasadila o 20 % více než Dana. Eva zasadila o 40 více než Dana. Zuzka zasadila toho co Dana.

Délka Odry na území Česka je 42 % její délky v Polsku. Celková délka toku od pramene do moře je 1 165 km.

Tyč je dlouhá 3 m.

Havarijní pojištění auta pana Jonáka stálo 14 050 Kč ročně. Pan Jonák díky provozu bez nehody získal již 40 % bonus (slevu).




Zvětšení lupy je 4násobné.

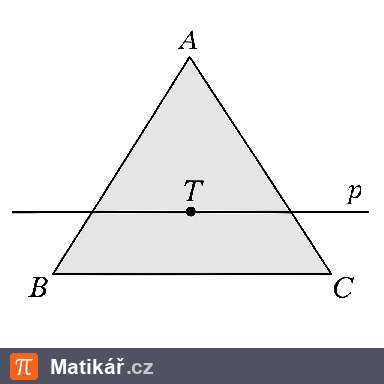
V trojúhelníku ABCE prochází přímka p těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC.


Lístek do kina stál 120 Kč. Potom ho zdražili o tři osminy z původní ceny.


V kocourkovském hradním muzeu byl nalezen větší počet středověkých kanónů vyrobených z děloviny (dělovina je slitina cínu a mědi v poměru 1:9). Kocourkovští radní se dohodli, že kanóny nepotřebují, ale hodil by se jim nový zvon do kocourkovské věže. Zvony se vyrábějí ze zvonoviny, která je také slitinou cínu a mědi, ale v poměru 1:4.

Jana, Martina a Zuzka si rozdělily bonbóny v poměru 3:7:5 . Martina dostala o 9 bonbonů méně než měly Jana a Zuzka spolu.
