Jolana rozdělovala bonbony. Čtvrtinu snědla, pětinu věnovala kamarádům. Zbytek bonbonů rozdělila na dvě stejné části a ty dala svým bratrům. Bratr Karel dostal 33 bonbonů.

Na čtyři porce je třeba nachystat 420 g masa. Budeme ale připravovat o tři porce více.

V hotelu bydlí polovina lidí v prvním patře, třetina ve druhém patře a zbylých 40 hostů v podkroví. Hotel je obsazen ze 75 %.

Digitální fotografie má rozměry 1 600×1 200 pixelů.
Průměrně se ze 100 litrů mléka vyrobí 16 litrů smetany a ze 100 litrů smetany se vyrobí 20 litrů másla.

Martina a Alena mají dohromady 114 bonbónů. Martina má 5krát více než Alena.

Petr se učil o čtvrtinu času více než Simona. Dohromady se učili 2 hodiny a 51 minut.

Martin měl třikrát více tyčinek než Arnošt, což bylo o 38 tyčinek víc.

Úhlopříčka televizní obrazovky je dlouhá 105 cm. Poměr stran je 4:3.

Bolek a Lolek měli každý svou aritmetickou posloupnost. Jak Lolkova, tak Bolkova posloupnost začínala číslem 2 023 a končila číslem 3 023. Tyto dvě posloupnosti měly 26 společných čísel. Poměr Bolkovy a Lolkovy diference byl 5:2.

Na mapě je skutečná vzdálenost 435 km mezi městy Paříž a Bern vyjádřena úsečkou 15 cm.

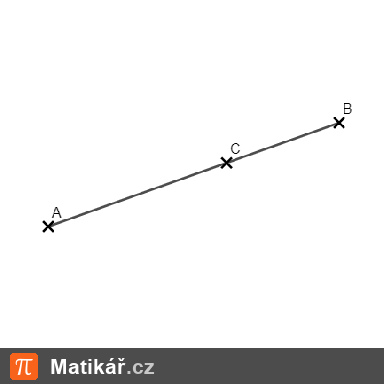
Délka úsečky |AB| = 14 cm. Na úsečce AB je zakreslen bod C tak, že velikosti úseček |AC| a |BC| jsou v poměru 4:3.
Na záchranu 160 stromů je třeba nasbírat 25 tun tříděného papíru.

Tři chlapci si měli rozdělit 1 813 Kč. Rozdělili si je v poměru Honza : Matěj 6:5. Matěj : Pavel 2:3.

Poměry stran pravoúhlého trojúhelníku jsou 3:4:5. Obvod trojúhelníka je 48 cm.

Tři společníci dostali za provedenou zakázku zaplaceno 90000 Kč. 40 % z této částky stal materiál, 23 % že zbylé částky odvedli za pojištění a daně. Zbytek peněz si rozdělili v poměru 2:3:5.

Petra, Jana a Martin nasbírali maliny v poměru 3:4:2 . Petra nasbírala 4,50 litrů malin.

Jeden potravinářský stroj vyrobí za hodinu 24 zákusků.

Obvod kosočtverce, který má délky úhlopříček v poměru 3:4 je 40 cm.
