Cena 1 kg hrušek je o 7 korun vyšší než cena 1 kg jablek. Prodejce prodal o 2 kg jablek více než hrušek. Za hrušky i jablka utržil shodné částky, a to 420 Kč.

Vstupenka do posilovny stojí 100 Kč za 90 minut. Se slevovou kartou zaplatí návštěvník za stejný čas 50 Kč. Cena slevové karty je 300 Kč.

Oddíl nakoupil trička bílá za 100 Kč za kus a černá 80 Kč za kus. Celkem to bylo 50 kusů za 4 200 Kč.

Petra, Jana a Martin nasbírali maliny v poměru 3:4:2 . Petra nasbírala 4,50 litrů malin.

Výletník šel po dobu 3 hodin rychlostí 4 km/h. Z důvodu zhoršujícího se počasí přidal do kroku a další hodinu a půl šel rychlostí 7 km/h. V závěru jeho výletu začalo pršet, tak se rozběhl a 30 minut běžel rychlostí 20 km/h.

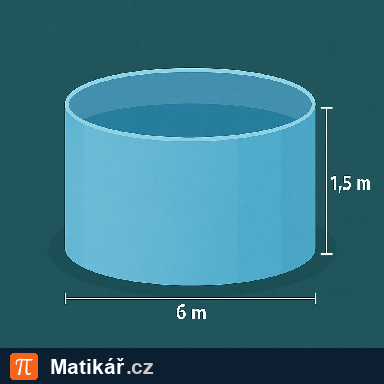
Zahradní bazén má tvar válce o průměru dna 6 m a výšce 1,50 m. Před prvním napuštěním byl natřen ochrannou barvou.

Do kolekce jsou smíchány dva druhy bonbónů. Kilogram prvního druhu stojí 360 Kč, kilogram druhého druhu stojí 540 Kč. Oba druhy jsou ve směsi zastoupeny v poměru 4:6.

Na jednu rybičku v akváriu je doporučené mít 3 litry vody. Akvárium má rozměry dna 80 × 50 cm a výškou 45 cm. Hladina vody sahá do výšky 5 cm pod horní okraj akvária.

V železářství prodávali 1 kg hřebíků za 400 Kč a 1 kg vrutů za 800 Kč. Celkem prodali 5 kg a utržili 3 200 Kč.

Délka Odry na území Česka je 42 % její délky v Polsku. Celková délka toku od pramene do moře je 1 165 km.


Zedník s učedníkem by společně postavili zeď za 15 hodin. Učedník sám by zeď postavil za 60 hodin.

Zvětšení lupy je 4násobné.

První čerpadlo naplní samostatně bazén za 7 hodin, druhé za 5 hodin.

Čísla A a B se liší o 95. Pokud od čísla A odečteme jeho dvě třetiny, dostaneme stejný výsledek, jako když k číslu B přičteme jeho tři pětiny.

Máme 6 kuliček různých barev. Najednou vybereme dvě kuličky.

Do 40 litrů vody je potřeba dát 0,60 litrů hnojiva.

Velikosti vnitřních úhlů α, β, γ trojúhelníku jsou v poměru 3:4:5.
Nina má dva malé sourozence, čtyřicetiměsíční Aničku a sedmiměsíčního Káju.
