Kvádr s rozměry dolní podstavy 45 cm a 10 cm má stejný objem jako krychle s hranou 30 cm³

Bazén s rozměry dna 3 m a 2 m je napuštěn 96 hl vody. Voda dosahuje 20 cm pod okraj bazénu.

V bazénu tvaru kvádru o rozměrech dna 12,50 m a 650 cm je 960 hl vody.

Pozemek má tvar pravoúhlého lichoběžníku se základnami 21 m a 11,20 m. Při ceně 2 500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1 352 400 korun.

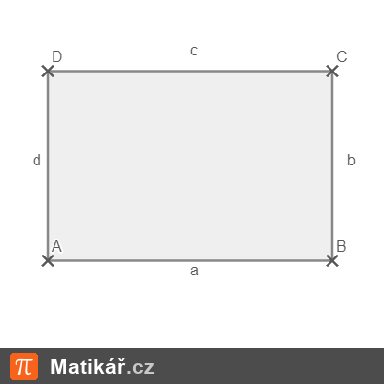
Obdélník má obvod 30 cm. Poměr délky a šířky je 2:3.
Karolína si koupila 5 trik a 2 mikiny. Jedno triko stálo 250 Kč. Karolína celkem zaplatila 2 210 Kč.

Pravidelný čtyřboký jehlan má objem 2 160 litrů a délku podstavné hrany 12 dm.

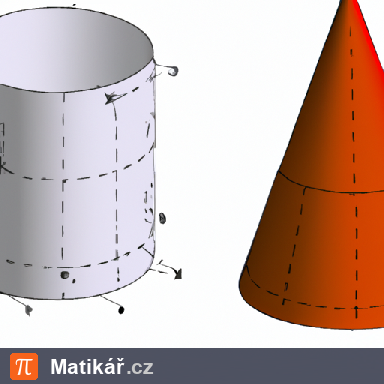
Rotační válec má objem 120 dm3. Rotační kužel má stejně velký objem i poloměr podstavy jako rotační válec.
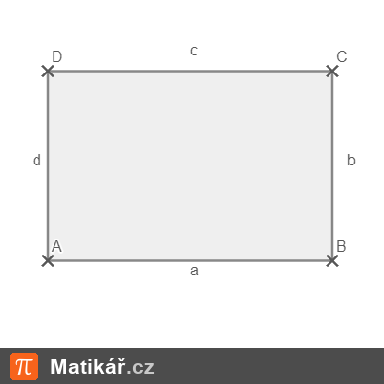
Obsah obdélníku je 81,25 cm2. Zvětšíme-li jeho délku o 5 mm, zvětší se jeho obsah o 4 %.
Krychli o objemu 4 096 cm3 je opsána a vepsána koule.

Je dán rovnoběžník ABCD, délka jeho jedné úhlopříčky je rovna délce jeho jedné strany.
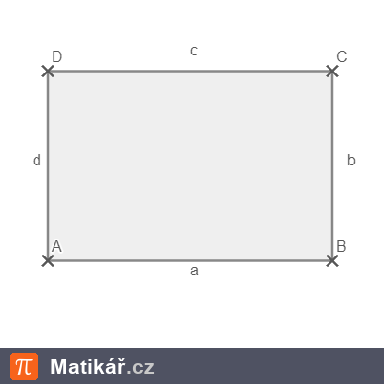
Objem pravidelného čtyřbokého jehlanu je 288 dm³. Obvod jeho podstavy je stejně velký jako jeho výška.

Pozemek tvaru pravoúhlého lichoběžníku má základny dlouhé 102 m a 86 m. Kolmé rameno má délku 63 m.

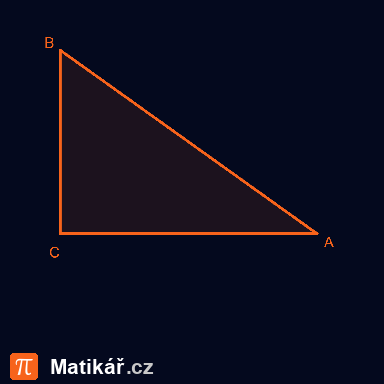
Délky stran pravoúhlého trojúhelníku tvoří první 3 členy aritmetické posloupnosti. Obsah trojúhelníku je 600 cm2.
V 6 hodin 30 minut vyplul z přístavu parník plující rychlostí 12 km/hod. Přesně v 10 hodin za ním vyplul motorový člun, který plul konstantní rychlostí 40 km/hod.

Jedna strana obdélníku má délku 18 cm. Obvod obdélníku je 48 cm.
Automobil projel jeden okruh neznámou stálou rychlostí, další dva stejné okruhy stálou rychlostí 72 km/hod. Celková průměrná rychlost byla 36 km/hod.

V továrně vyrobí 12 linek dané množství šroubů za 16 dní.

Kolmý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikla ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3 cm a 4 cm. Výška hranolu je 8 cm.
