Úlohy: 1–20 / 126

12345
Přehled ročníků

1. Dělitelnost devítkou

Napište co nejmenší číslo, které je větší než 7 825 a je beze zbytku dělitelné 9.
Řešení
Jde o číslo 7 830.
Matematická úloha – Dělitelnost devítkou

2. Vzdálenost na číselné ose

Vypočítejte, které číslo je na číselné ose stejně vzdáleno od čísel 5,30 a 7,70.
Řešení
Číslo 6,50 je na číselné ose stejně vzdáleno od čísel 5,30 a 7,70.
Matematická úloha – Vzdálenost na číselné ose

3. Doprava na exkurzi

Ředitel pořádá exkurzi pro více než 400 studentů. Odvoz již zajistil pro 280 studentů. Každý školní autobus má kapacitu pro přepravu 40 studentů.

Vypočítejte, kolik školních autobusů je ještě potřebných pro přepravu všech studentů.
Řešení
Pro přepravu zbývajících studentů jsou potřeba ještě 3 školní autobusy.
Matematická úloha – Doprava na exkurzi

4. Oslava narozenin tety a srýce

Strýc Anety má narozeniny ve stejný den v roce jako Anetčina teta. Strýc je starší než teta, ne však o víc než o 10 let, a oba jsou plnoletí (starší než 18 let). Na poslední oslavě jejich narozenin si Aneta uvědomila, že když vynásobí jejich oslavované věky a výsledný součin ještě vynásobí počtem psů, kteří se na oslavě sešli, dostane číslo 2 024.

Určete. kolik psů mohlo být na této oslavě. (Uveďte všechny možnosti.)
Řešení
Na oslavě může být 1 pes nebo 4 psi.
Matematická úloha – Oslava narozenin tety a srýce

5. Absolutní hodnota

Vypočítejte
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   16
b)   8
c)   19
d)   28
e)   7
f)   19
Matematická úloha – Absolutní hodnota

6. Absolutní hodnota

Vypočítejte
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   14
b)   9
c)   5
d)   32
e)   32
f)   11
Matematická úloha – Absolutní hodnota

7. Zkrácení prkna

Prkno dlouhé m bylo zkráceno o m.

Vypočítejte, jak dlouhé bylo prkno po odříznutí.
Řešení
Prkno bylo dlouhé m.
Matematická úloha – Zkrácení prkna

8. Turista na cestě

Turista šel cesty rychlostí 6 km/hod, cesty rychlostí 4 km/hod a zbývajících 7 km rychlostí 5 km/hod.

Vypočítejte:
a)   kolik kilometrů turista ušel,
b)   kolik minut mu trvala cesta.
Řešení
a)   Turista ušel 20 kilometrů.
b)   Cesta mu trvala 254 minut.
Matematická úloha – Turista na cestě

9. Vypočítejte rovnici

Vypočítejte rovnici a udělejte zkoušku.
Řešení
x = 4
Matematická úloha – Vypočítejte rovnici

10. Pět hodů mincí

Vypočítejte, jaká je pravděpodobnost, že při hodu mincí 5× po sobě padne hlava. (Výsledek zapište ve tvaru zlomku.)
Řešení
Pravděpodobnost je .
Matematická úloha – Pět hodů mincí

11. Mzda Soni

Soňa obdržela zaplaceno 150 Kč za hodinu a 70 Kč za Každou odpracovanou hodinu nad 40 hodin týdně. V pondělí odpracovala 12 hodin, v úterý 7 hodin, ve středu 9 hodin, ve čtvrtek 8 hodin a v pátek 10 hodin.

Vypočítejte, jaká byla celková mzda Soni za týden.
Řešení
Celková mzda Soni za celý týden byla 7 320 Kč.
Matematická úloha – Mzda Soni

12. Lenčiny kuličky

Lenka má 180 kuliček. z nich je modrých, červených, zelených a zbytek žlutých.

Vypočítejte, kolik má Lenka žlutých kuliček.
Řešení
Lenka tedy má 27 žlutých kuliček.
Matematická úloha – Lenčiny kuličky

13. Praní prádla

Roman a Tomáš si dnes prali prádlo. Ronald peří každých 6 dní a Tim každých 9 dní.

Vypočítejte, kolik dní bude trvat, než Roman a Tomáš budou prát tentýž den.
Řešení
Bude to trvat 18 dní.
Matematická úloha – Praní prádla

14. Kužel a válec

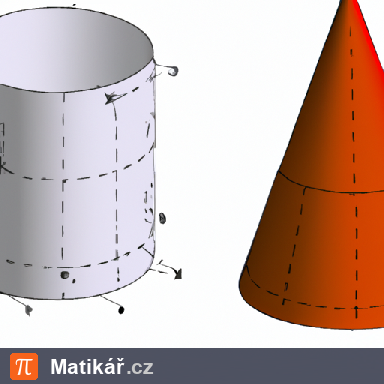
Rotační válec má objem 120 dm3. Rotační kužel má stejně velký objem i poloměr podstavy jako rotační válec.

Vypočítejte, o kolik procent je větší výška rotačního kužele než výška rotačního válce.
Řešení
Výška rotačního kužele je větší o 200 %.
Matematická úloha – Kužel a válec

15. Násobení zlomků

Vypočítejte a zapište v základním tvaru:
a)   \[ \frac{8}{12} \cdot \frac{1}{5} = \]
b)   \[ \frac{3}{9} \cdot \frac{1}{11} = \]
c)   \[ \frac{2}{7} \cdot \frac{7}{9} = \]
d)   \[ \frac{8}{10} \cdot \frac{4}{7} = \]
e)   \[ \frac{4}{5} \cdot \frac{3}{8} = \]
f)   \[ \frac{6}{14} \cdot \frac{2}{9} = \]
Řešení
a)   \[ \frac{2}{15} \]
b)   \[ \frac{1}{33} \]
c)   \[ \frac{2}{9} \]
d)   \[ \frac{16}{35} \]
e)   \[ \frac{3}{10} \]
f)   \[ \frac{2}{21} \]
g)   \[ \frac{1}{6} \]
Matematická úloha – Násobení zlomků

16. Řezání dřevěné tyče

Dřevěná tyč byla rozřezána na tři části. První část měřila jednu třetinu délky, druhá jednu třetinu zbytku a třetí část 20 cm.

Vypočítejte:
a)   v cm původní délku tyče,
b)   v cm délky jednotlivých částí.
Řešení
a)   Původní délka tyče byla 45 cm.
b)   První část měřila 15 cm, druhá část 10 cm a třetí část 20 cm.
Matematická úloha – Řezání dřevěné tyče

17. Po sobě jdoucí čísla

Součet tří po sobě jdoucích čísel je 183.

Určete, o jaká čísla jde.
Řešení
Jsou to čísla 60, 61 a 62.
Matematická úloha – Po sobě jdoucí čísla

18. Rozdělení čísla

Rozdělte číslo 85 na dvě části tak, aby poměr těchto částí byl 8:9.
Řešení
Části jsou 40 a 45.
Matematická úloha – Rozdělení čísla

19. Sýkorky na stromech

Na tři stromy přiletělo 36 sýkorek. Když z prvního stromu přeletělo na druhý

strom 6 sýkorek a z druhého stromu na třetí 4 sýkorky, bylo na všech stromech

stejně sýkorek.

Vypočítejte, kolik sýkorek sedělo původně na každém stromě.
Řešení
Na prvním stromě bylo 18 sýkorek, a druhém stromě bylo 10 sýkorek a na třetím stromě bylo 8 sýkorek
Matematická úloha – Sýkorky na stromech

20. Dvě cesty Kamily

Kamila cestovala na své první cestě hodiny a na druhé hodiny.

Vypočítejte, o kolik více času strávila Kamila na druhé cestě více než na první.
Řešení
Kamila strávila na druhé cestě o hodiny více než na první.
Matematická úloha – Dvě cesty Kamily
 
12345