




Součet pěti po sobě jdoucích přirozených čísel je 555.

Je dán výraz 3x – [2 – (2x – 1) + x].
Karel má v pokladničce celkem 19 mincí, a to pouze desetikorunové a padesátikorunové mince. Celkem má v pokladničce naspořeno 830 Kč.

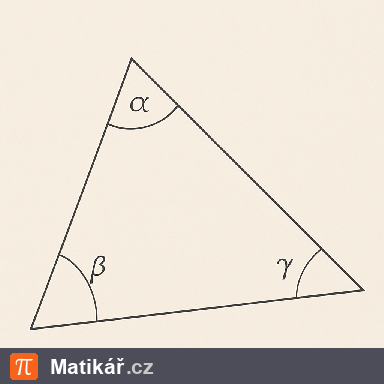
Velikosti vnitřních úhlů α, β, γ trojúhelníku jsou v poměru 3:4:5.
Nina má dva malé sourozence, čtyřicetiměsíční Aničku a sedmiměsíčního Káju.

Uzavřená krabice má tvar kolmého hranolu s podstavou rovnostranného trojúhelníku. Hrana podstavy je 24 cm dlouhá, výška krabice je 0,50 m.

Bylo zjištěno, že na jeden kilogram masa je zapotřebí 6,50 kg obilí, 36 kg krmné směsi a 15 m3 vody. Plátek hovězího masa váží v syrovém stavu 45 gramů.

Součet tří po sobě jdoucích sudých čísel je roven 978.

Zboží, podnikatel prodává za 700 Kč, nakoupil ve velkoskladu za 500 Kč.

Anička a Katka bydlí v obcích vzdálených od sebe 18 km. Dohodly se, že se setkají přesně v polovině cesty. Anička šla rychlostí 6 km/h. Katka se zdržela a o 30 minut později vyrazila na kole.

Nádoba tvaru krychle má bez víka povrch 320 centimetrů2.

Kamarádky Pavla, Petra a Sára si šly zacvičit. Celkem cvičily 360 minut. Pavla cvičila trojnásobek času oproti každé ze svých dvou kamarádek. Petra a Sára cvičily stejný čas.

4 dělníci vyrobí za 8 dní 960 výrobků.

Denní normovaný výkon pracovníka předpokládá vyrobení 530 součástek stejného druhu. Skutečný výkon pracovníka byl 702 součástek.

Písařka napsala na stroji 24 stran textu za 2 hodiny 40 minut.
