
Je dán pravidelný šestiúhelník ABCDEF.

Na houpačce, kterou je páka se dvěma rameny, sedí dvě děti. Houpačka je v rovnováze. Na levé straně sedí 150 cm od středu dítě s hmotností 30 kg a na pravé dítě s hmotností 20 kg.

Olga jela na projížďku na kole. Za hodinu se za ní po stejné trase vypravil bratr na motorce stálou rychlostí 60 km/h a dojel ji za hodiny.

Notebook před byl zdražen o 15 % a nyní ho doprodávají za 13 800 Kč, což je 80 % zdražené ceny.



Úhlopříčka televizní obrazovky je 84 cm a výška je 40 cm.

Cesta má dvě části v celkové délce 190 metrů. Delší část cesty je o 10 metrů kratší než trojnásobek délky kratší části cesty.

Kamarádi Petr a Martin bydlí ve vzdálenosti 13 kilometrů od sebe. Petr jel za Martinem na kole průměrnou rychlostí 18 km/hod. a Martin mu ve stejném okamžiku vyjel naproti na koloběžce. Za půl hodiny po vyjetí se setkali.

Měřítko mapy je 1:100 000. Vzdušná vzdálenost mezi dvěma městy měří na mapě 25 cm. Vzdálenost dvou obcí ve skutečnosti je 8 km.

Lístek do kina stál 120 Kč. Potom ho zdražili o tři osminy z původní ceny.

Z měst A a B, která jsou od sebe vzdálena 50 km, vyrazila proti sobě ve stejném čase dvě auta průměrnými rychlostmi 80 km/h (z měta A) a 120 km/h (z města B).


V košíku je pět červených jablek průměrné hmotnosti 125 gramů a jedno žluté jablko. Průměrná hmotnost všech jablek v košíku je 120 gramů.


V kocourkovském hradním muzeu byl nalezen větší počet středověkých kanónů vyrobených z děloviny (dělovina je slitina cínu a mědi v poměru 1:9). Kocourkovští radní se dohodli, že kanóny nepotřebují, ale hodil by se jim nový zvon do kocourkovské věže. Zvony se vyrábějí ze zvonoviny, která je také slitinou cínu a mědi, ale v poměru 1:4.

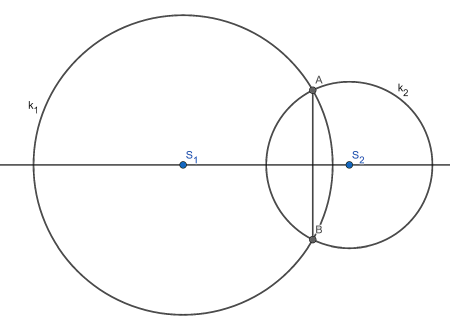
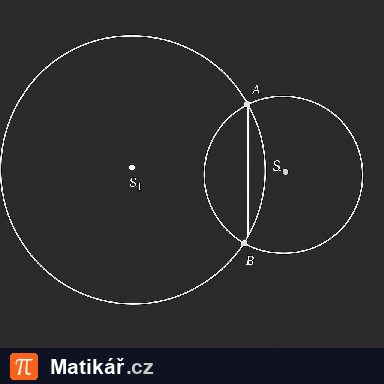
Na obrázku jsou kružnice k₁(S₁; r₁ = 9 cm) a k₂(S₂; r₂ = 5 cm). Jejich průsečíky určují společnou tětivu AB dlouhou 8 cm.
Máme 2 stejné modré kuličky a 2 stejné červené kuličky. Uspořádáme je všemi způsoby do řady.

Do 40 litrů vody je potřeba dát 0,60 litrů hnojiva.
