Barva se prodává v plechovce tvaru válce s výškou 24,50 cm a s průměrem 15 cm. Plná plechovka váží 5,50 kg.


Příkop o průřezu tvaru rovnoramenného lichoběžníku o základnách 3 m a 5 m a ramenech o délce 2 m je hluboký 2,50 metru a dlouhý 10 metrů.

Kolmý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikla ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3 cm a 4 cm. Výška hranolu je 8 cm.

Je dán kvádr s rozměry 54,50 cm, 12,70 cm, 32,30 cm.
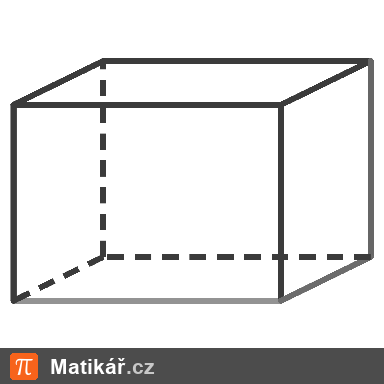
Kvádr má délku 12 cm, šířku 0,60 dm. Výška má stejnou velikost jako hrana krychle, jejíž objem je 64 cm3.
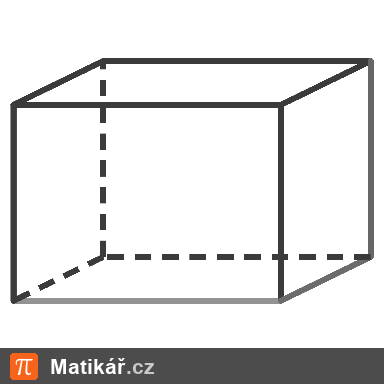
Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.

Střecha věže má tvar pravidelného čtyřbokého jehlanu a výškou 4 m a hranou podstavy 6 m. Zjistilo se, že je poškozeno 25 % krytiny na střeše.

Krabice má výšku 55 cm a šířku 40 cm. Objem krabice je 180 litrů.

Je dán pravidelný čtyřbokého jehlanu. Výška jehlanu je 30 cm a stěnová výška je 50 cm.

Na jednu rybičku v akváriu je doporučené mít 3 litry vody. Akvárium má rozměry dna 80 × 50 cm a výškou 45 cm. Hladina vody sahá do výšky 5 cm pod horní okraj akvária.



Uzavřená krabice má tvar kolmého hranolu s podstavou rovnostranného trojúhelníku. Hrana podstavy je 24 cm dlouhá, výška krabice je 0,50 m.

Nádoba tvaru krychle má bez víka povrch 320 centimetrů2.

Akvárium má rozměry podstavy 80 cm a 45 cm a je v něm 72 litrů vody.

Krychle má povrch 486 dm2.


Krabice má tvar kvádru o rozměrech 3 cm, 4 cm a 5 cm.

Čtyřboký hranol má objem 720 cm3. Podstavu tvoří kosodélník se stranou dlouhou 16 cm a příslušnou výškou 5 cm.
