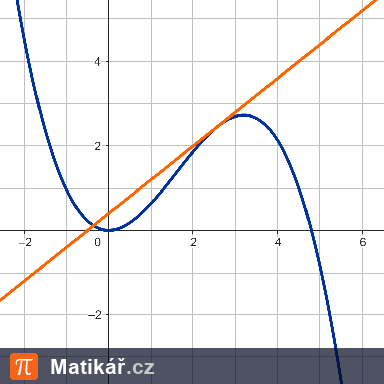
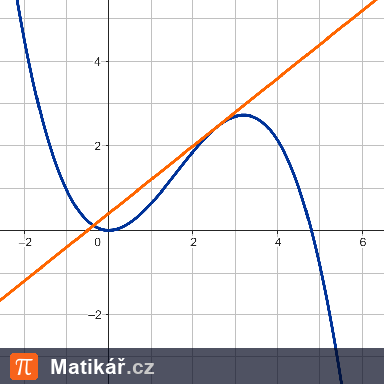
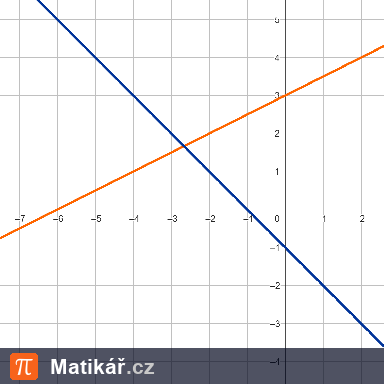
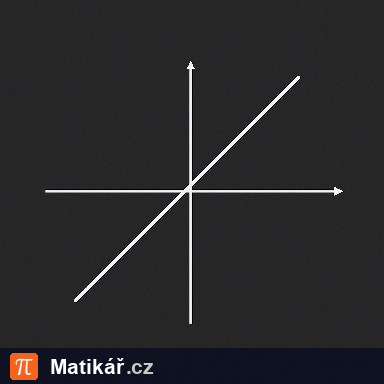
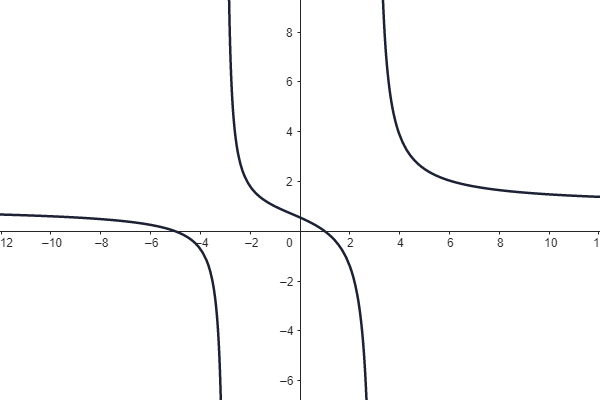
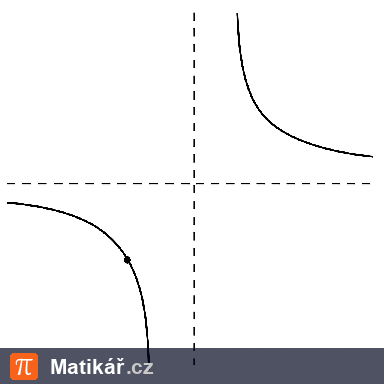
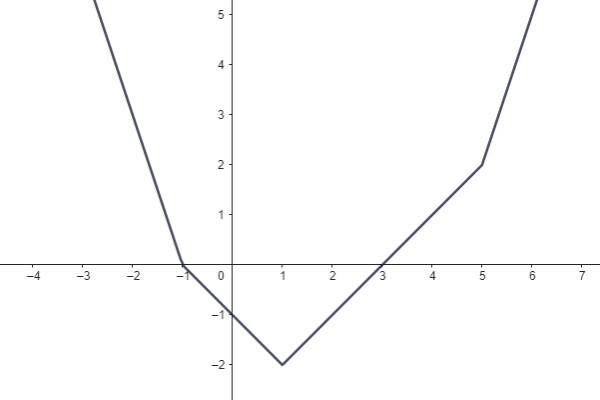
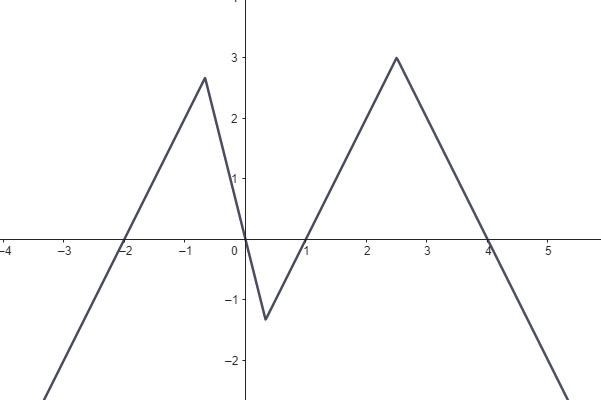
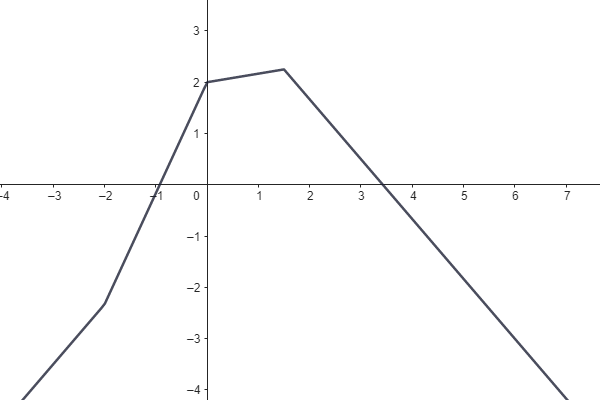
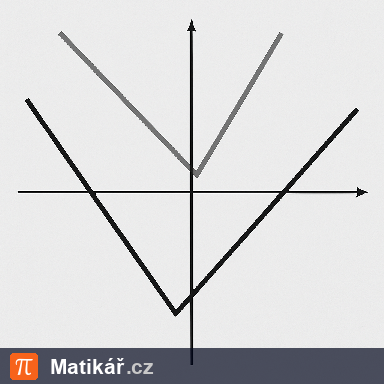
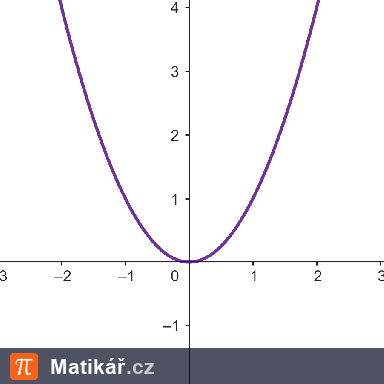
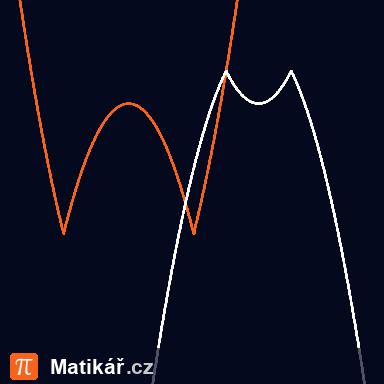
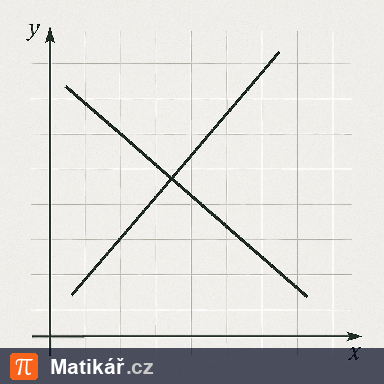
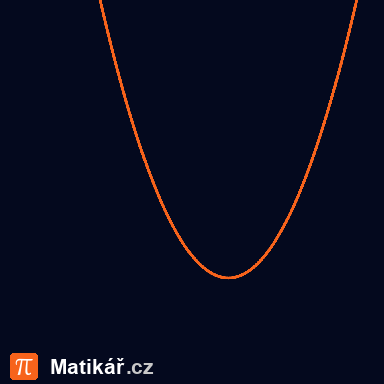
a) definiční obor funkce f,
b) obor hodnot funkce f,
c) průsečík grafu funkce f s osou y (pokud existuje),
d) průsečíky grafu funkce f s osou x (pokud existují),
e) zda je funkce f sudá nebo lichá,
f) zda je funkce f periodická,
g) zda je funkce f prostá,
h) zda je funkce f ohraničená zdola nebo shora,
i) intervaly spojitosti funkce f,
j) první derivaci funkce,
k) druhou derivaci funkce,
l) stacionární body,
m) lokální extrémy funkce,
n) v kterých intervalech funkce f roste,
o) v kterých intervalech funkce f klesá,
p) inflexní body,
q) intervaly konvexnosti funkce,
r) intervaly konkávnosti funkce,
s) asymptoty funkce (pokud existují),
t) limity na hranicích definičního oboru,
u) načrtněte graf funkce.