V továrně vyrobí 12 linek dané množství šroubů za 16 dní.

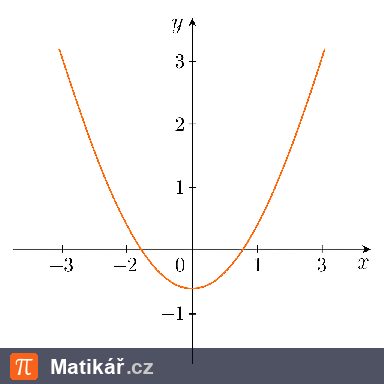
Graf kvadratické funkce prochází body A[1;1], B[3;-1] a C[1;2].
Čarodějnice připravuje lektvar věčného mládí. V receptu se dočetla, že objem lektvaru je tvořen ze dvou devítin z tekutého jedu ropuchy, z šesti patnáctin z nektaru mandragory a zbytek tvoří 34 mililitrů vody.

Je dáno číslo 123 456 789


Tři strážní mají společnou ostrahu podniku. První vykoná svoji pochůzku za 15 minut, druhý ujde svůj okruh za 10 minut a třetí strážný za 12 minut.

Na školním lyžařském výletě vyjelo z chaty v 8 h 30 min. družstvo rychlostí 2 m/s. V 8 h 45 min. minut později za nimi vyjel stejnou trasou instruktor rychlostí 3 m/s.
Je dáno číslo 346

Jsou dána čísla 22, 368, 400, 602, 699, 978, 12 334.

Matěj dokáže vyčistit pozemek za 20 minut. Miloš dokáže vyčistit tentýž pozemek za 30 minut.


Je třeba naskládat obdélníky o rozměrech 210 mm a 84 mm tak, aby zakryly čtverec.

Učitel napsal na tabuli číslo menší než 50 000.
První žák řekl: "Toto číslo je dělitelné 2."
Druhý žák řekl: "Toto číslo je dělitelné 3."
A tak dále, až po posledního, který tvrdil, že je dělitelné 13. Jeden žák ale lhal.

Ve městě se rozhodli, že postaví dětské a volejbalové hřiště. Volejbalové bude mít rozměr 12 m × 18,75 m. Dětská hřiště bude mít tvář čtverce. Plocha obou hřišť bude stejná.


Truhlář má tři desky dlouhé 360 cm, 27 dm a 450 cm. Chce z nich nařezat stejně dlouhé desky tak, aby nezůstaly žádné zbytky.

Na hodinovém ciferníku navzájem spojíme body u čísel 3, 10 a 12, čímž vznikne trojúhelník.

Jedna strana obdélníku měří 35 cm a druhá je o 7 cm kratší než úhlopříčka obdélníku.
Obsah lichoběžníku je 111,80 cm2 a jeho výška 6,50 cm.