Zvětšení lupy je 4násobné.

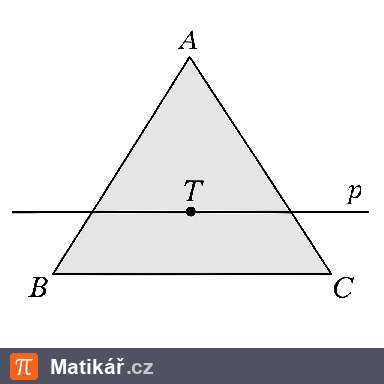
V trojúhelníku ABCE prochází přímka p těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC.

Kamarádi Petr a Martin bydlí ve vzdálenosti 13 kilometrů od sebe. Petr jel za Martinem na kole průměrnou rychlostí 18 km/hod. a Martin mu ve stejném okamžiku vyjel naproti na koloběžce. Za půl hodiny po vyjetí se setkali.

V hnízdě seděla ptáčata. Pak 2 sežrala kočka a dvě pětiny zbylých ptáčat uletěly. V hnízdě zůstalo 6 ptáčat.

Z měst A a B, která jsou od sebe vzdálena 50 km, vyrazila proti sobě ve stejném čase dvě auta průměrnými rychlostmi 80 km/h (z měta A) a 120 km/h (z města B).

Čísla A a B se liší o 95. Pokud od čísla A odečteme jeho dvě třetiny, dostaneme stejný výsledek, jako když k číslu B přičteme jeho tři pětiny.

V košíku je pět červených jablek průměrné hmotnosti 125 gramů a jedno žluté jablko. Průměrná hmotnost všech jablek v košíku je 120 gramů.


V osudí je 5 bílých a 9 černých koulí. Namátkou vybereme tři koule.






Akvárium má rozměry podstavy 80 cm a 45 cm a je v něm 72 litrů vody.

4 dělníci vyrobí za 8 dní 960 výrobků.

Denní normovaný výkon pracovníka předpokládá vyrobení 530 součástek stejného druhu. Skutečný výkon pracovníka byl 702 součástek.

První den bylo třeba přepravit 240 lidí, dvěma autobusy trvala přeprava 30 minut.

Kilogram jahodových bonbónů stojí 160 Kč, kilogram malinových bonbónů stojí 200 Kč/kg. Cukrář má připravit 20 kg směsi v ceně 190 Kč/kg. Cena směsi se stanovuje podle poměru, v jakém se bonbóny míchají.
