obsah

Příkop o průřezu tvaru rovnoramenného lichoběžníku o základnách 3 m a 5 m a ramenech o délce 2 m je hluboký 2,50 metru a dlouhý 10 metrů.

Ve městě se rozhodli, že postaví dětské a volejbalové hřiště. Volejbalové bude mít rozměr 12 m × 18,75 m. Dětská hřiště bude mít tvář čtverce. Plocha obou hřišť bude stejná.

Je dán trojúhelník ABC. Jeho obvod je 30 cm, přičemž strana a je o 2 cm delší než strana b a o 5 cm kratší než strana c.

Je dán kvádr s rozměry 54,50 cm, 12,70 cm, 32,30 cm.

Obsah lichoběžníku je 111,80 cm² a jeho výška 6,50 cm.

Obvod kosočtverce, který má délky úhlopříček v poměru 3:4 je 40 cm.

Pozemek, na kterém se má stavět rodinný dům, má tvar lichoběžníku se základnami o délce 42 m a 18 m, vzdálenost základen je 23 m. Dům bude mít podle projektu 146 m² zastavěné plochy.

Nádrž tvaru válce o průměru 100 cm je naplněná z 50 % a je v ní 78 500 l vody.

Zahrada ve tvaru čtverce má stranu 27 metrů dlouhou.

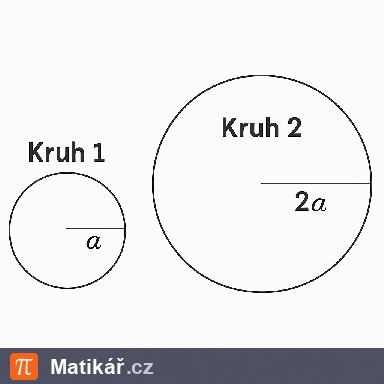
Kruh 1 má poloměr a. Kruh 2 má poloměr dvakrát větší.

Na pozemku tvaru obdélníku stojí lesní školka. Jedna strana pozemku měří 12 m, druhá o 3 m více.

Vzájemná vzdálenost stromků je 1 m a na všech stranách 1 m od plotu.

Cena sloupku na oplocení je 200 Kč a 1 m pletiva stojí 80 Kč. Vzdálenosti mezi sloupky jsou 3 m.

Výměra obdélníkového pozemku o délce 70 m je 2 800 m².

Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,30 m. Odchylka strany od roviny podstavy je 36 °.

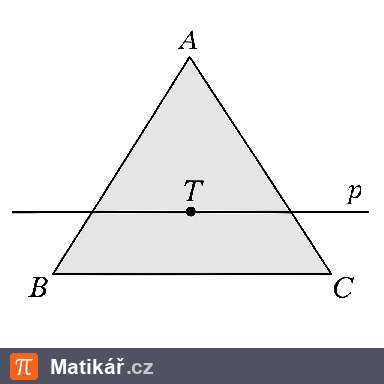
V trojúhelníku ABCE prochází přímka p těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC.

Podlaha koupelny má tvar obdélníku o rozměrech 2 metry a 2,50 metru. Je v ní vana o rozměrech dna 150 cm a 60 cm. Zbytek podlahy je pokryt krásnými kachličkami.

Uzavřená krabice má tvar kolmého hranolu s podstavou rovnostranného trojúhelníku. Hrana podstavy je 24 cm dlouhá, výška krabice je 0,50 m.

Nádoba tvaru krychle má bez víka povrch 320 centimetrů².