Úlohy: 1–7 / 7

1
Přehled ročníků

1. Exponenciální rovnice

Najděte řešení exponenciálních rovnic:
a)   
b)   
Řešení
a)   x = 5
b)   x = 3

2. Trosečník na ostrově

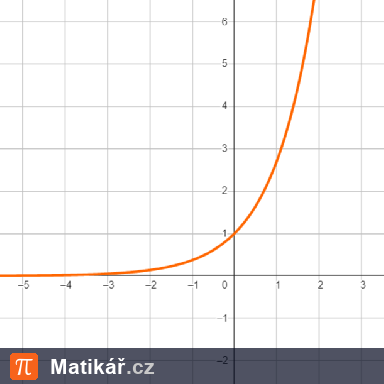
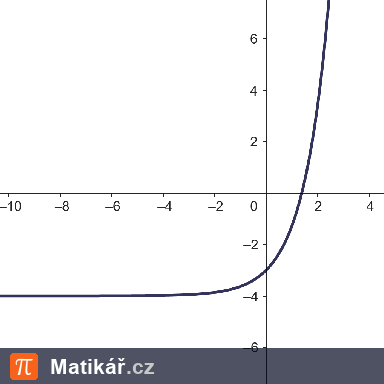
Trosečník přišel na pustý ostrov se 4 obilnými zrnky. Z jednoho zrnka získal 10 zrnek a na chléb potřeboval 1 kg obilí a 1 zrnko má hmotnost asi 0,20 g? (Předpokládejme jednu úrodu za rok.)

Vypočítejte, kolik let trosečníkovi trvalo, než si vypěstoval dost obilí na chléb.
Řešení
Trosečníkovi trvalo 4 roky, než si vypěstoval dost obilí na chléb.

3. Exponenciální rovnice

Řešte rovnice
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   

4. Kvadratické nerovnice

Řešte nerovnice v R
a)   
b)   
c)   
d)   
e)   
f)   
g)   
h)   
Řešení
a)   
b)   
c)   
d)   nemá řešení v R
e)   
f)   
g)   
h)   

5. Kvadratické nerovnice

Řešte nerovnice
a)   
b)   
c)   
d)   
e)   
f)   
Řešení
a)   
b)   
c)   
d)   
e)   
f)   

6. Získaný úrok

Za kolik let vynese jistina 50000 Kč při 5 % p. a. úrok 5125 Kč?

Řešení
Počet let je 2.

7. Bakterie ve zkumavce

Bakterie ve zkumavce se dělí každou sekundu na dvě, přičemž každá nová má stejný objem jako původní. Přesně o půlnoci byla zkumavka plná.

Kolik sekund před půlnocí byla zkumavka zaplněna do poloviny?
Řešení
Počet sekund před půlnocí, kdy byla zkumavka zaplněná do poloviny, bylo 1.
 
1