Krabičky o rozměrech 6 cm, 10 cm, 15 cm se mají rovnat do krabice tvaru krychle.

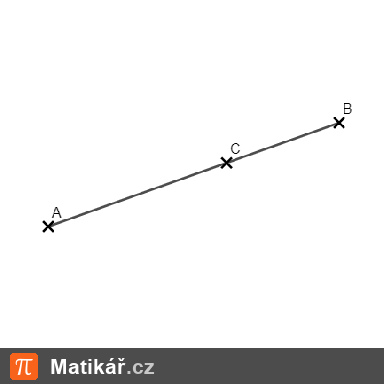
Délka úsečky |AB| = 14 cm. Na úsečce AB je zakreslen bod C tak, že velikosti úseček |AC| a |BC| jsou v poměru 4:3.
Je dáno číslo 123 456 789

Tři chlapci si měli rozdělit 1 813 Kč. Rozdělili si je v poměru Honza : Matěj 6:5. Matěj : Pavel 2:3.

Na oslavu Jardových narozenin se sešlo 24 hostů. Polovina z nich byli bývalí spolužáci, čtvrtina byli spoluhráči z fotbalu a třetina byli sousedi.

Tři společníci dostali za provedenou zakázku zaplaceno 90000 Kč. 40 % z této částky stal materiál, 23 % že zbylé částky odvedli za pojištění a daně. Zbytek peněz si rozdělili v poměru 2:3:5.
Paní Tučná chce zhubnout v lednici má maso o hmotnosti kilogramu. Paní Tučná má však povoleno sníst v rámci diety pouze
kilogramu masa.

Na stole jsou dvě krabice pizzy stejné velikosti. V jedné krabici je pizzy a ve druhé
pizzy. Potom kuchař rozdělí obě pizzy na dílky tak, že jeden dílek je
pizzy.

Za 10 let bude papoušek 3krát starší než dnes.

Truhlář má tři desky dlouhé 360 cm, 27 dm a 450 cm. Chce z nich nařezat stejně dlouhé desky tak, aby nezůstaly žádné zbytky.

Petra, Jana a Martin nasbírali maliny v poměru 3:4:2 . Petra nasbírala 4,50 litrů malin.

Pokladník má vyplatit následující částky:
369 Kč, 1 426 Kč, 694 Kč, 1 242 Kč, 858 Kč a 219 Kč.

Na jednu rybičku v akváriu je doporučené mít 3 litry vody. Akvárium má rozměry dna 80 × 50 cm a výškou 45 cm. Hladina vody sahá do výšky 5 cm pod horní okraj akvária.

Tyč je dlouhá 3 m.


Tři tyče o délkách 24 dm, 3 m a 160 cm mají být rozřezány na stejně dlouhé části tak, aby byly co nejdelší.

Je dán pravidelný šestiúhelník ABCDEF.



