Matikář - Úlohy na procvičení

Úlohy: 1–20 / 24

1. Průsečík dvou rovin

Najděte průsečík rovin:

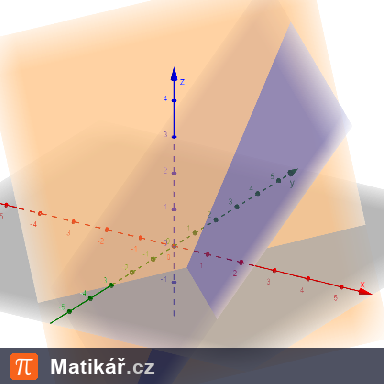
a) \[ \text{Rovina } \rho_1 \text{: } x = 2 + s, \quad y = s + t, \quad z = 3 + t, \quad s, t \in \mathbb{R}.\] \[ \text{Rovina } \rho_2 \text{: } x = 4 + u, \quad y = 2u - v, \quad z = 5 - v, \quad u, v \in \mathbb{R}. \]

b) \[ \text{Rovina } \rho_1 \text{: } x = s, \quad y = 2 + s + t, \quad z = 3 + t, \quad s, t \in \mathbb{R}. \] \[ \text{Rovina } \rho_2 \text{: } x = u + v, \quad y = 4 - u, \quad z = 6 + v, \quad u, v \in \mathbb{R}. \]

c) \[ \text{Rovina } \rho_1 \text{: } x = 3 + s, \quad y = -s, \quad z = 2 - t, \quad s, t \in \mathbb{R}. \] \[ \text{Rovina } \rho_2 \text{: } x = 3 + 2u - v, \quad y = u - 2v, \quad z = 2 + u + v, \quad u, v \in \mathbb{R}. \]

d) \[ \text{Rovina } \rho_1 \text{: } x = 1 + s, \quad y = 1 + t, \quad z = 1 + t, \quad s, t \in \mathbb{R}.\] \[ \text{Rovina } \rho_2 \text{: } x = 2 + u, \quad y = 2 - v, \quad z = 2 - v, \quad u, v \in \mathbb{R}. \]

Řešení

a) \[ x = 4, \quad y = 8 - v, \quad z = 5 - v, \quad v \in \mathbb{R}. \]

b) \[ x = -\frac{1}{2} + v, \quad y = \frac{9}{2} + v, \quad z = 6 + v, \quad v \in \mathbb{R}. \]

c) \[ x = 3 + v, \quad y = -v, \quad z = 2 + 2v, \quad v \in \mathbb{R}. \]

d) \[ x = 1 + v, \quad y = 2 - v, \quad z = 2 - v, \quad v \in \mathbb{R}. \]

2. Limity funkcí

Pomocí l'Hospitalova pravidla vypočítejte limity funkcí:

a) \[\lim_{x \to \infty} \frac{x}{e^x}\]

b) \[\lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x}}\]

c) \[\lim_{x \to 0} \frac{\sin(x)}{x^2}\]

d) \[\lim_{x \to 1} \frac{x^2 - 1}{x - 1}\]

e) \[\lim_{x \to \infty} \frac{\ln(x)}{\sqrt{x}}\]

f) \[\lim_{x \to 0} \frac{\tan(x)}{x}\]

Řešení

a) 0

b) 0

c) 0

d) 2

e) 0

f) 1

3. Derivace funkcí

Vypočítejte derivace následujících funkcí:

a) \[ f(x) = x^2 \cdot e^x \]

b) \[ g(x) = \frac{x^2 + 3}{x - 1} \]

c) \[ h(x) = \sin(x) \cdot \cos(x) \]

d) \[ k(x) = \sqrt{x^2 + 1} \]

e) \[ m(x) = e^{\sin(x)} \]

f) \[ p(x) = \ln(x^2 + 1) \]

Řešení

a) \[ f'(x) = e^x (2x + x^2) \]

b) \[g'(x) = \frac{x^2 - 2x - 3}{(x - 1)^2}\]

c) \[h'(x) = \cos(2x)\]

d) \[k'(x) = \frac{x}{\sqrt{x^2 + 1}}\]

e) \[m'(x) = e^{\sin(x)} \cos(x)\]

f) \[p'(x) = \frac{2x}{x^2 + 1}\]

4. Integrál metodou per partes

Integrujte metodou per partes:

a) $\int x \sin(x) \, dx$

b) $\int x e^x \, dx$

c) $\int \ln(x) \, dx$

d) $\int x^2 \cos(x) \, dx$

e) $\int x \ln(x) \, dx$

f) $\int e^x \cos(x) \, dx$

Řešení

a) \[-x \cos(x) + \sin(x) + C\]

b) \[x e^x - e^x + C\]

c) \[x \ln(x) - x + C\]

d) \[x^2 \sin(x) + 2x \cos(x) - 2 \sin(x) + C\]

e) \[\frac{x^2}{2} \ln(x) - \frac{x^2}{4} + C\]

f) \[\frac{1}{2} e^x (\cos(x) - \sin(x)) + C\]

5. Sarrusovo pravidlo

Vypočítejte determinant pomocí Sarrusova pravidla:

a) \[ \begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} \]

b) \[ \begin{vmatrix} 2 & 1 & 3 \\ 1 & 4 & 2 \\3 & 5 & 6 \end{vmatrix}\]

c) \[ \begin{vmatrix} 3 & 0 & 1 \\ 2 & 4 & 5 \\ 1 & 3 & 2 \end{vmatrix}\]

d) \[ \begin{vmatrix}1 & 3 & 5 \\2 & 1 & 4 \\3 & 2 & 1\end{vmatrix}\]

e) \[ \begin{vmatrix} 5 & 2 & 0 \\ 1 & 3 & 2 \\ 4 & 1 & 3\end{vmatrix}\]

f) \[\begin{vmatrix}1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \end{vmatrix}\]

Řešení

a) $ 0 $

b) $ 7 $

c) $ -19 $

d) $ 28 $

e) $ 45 $

f) $ 1 $

6. Limity posloupností 2

Vypočítejte následující limity:

a) \[\lim_{n \to \infty} \frac{3n^2 + 5}{n^2 + 4n + 1}\]

b) \[\lim_{n \to \infty} \frac{n + \ln n}{n + 1}\]

c) \[\lim_{n \to \infty} \frac{\cos n}{n^2}\]

d) \[\lim_{n \to \infty} \frac{n^3}{n^2 + 1}\]

e) \[\lim_{n \to \infty} \left(1 - \frac{2}{n}\right)^n\]

f) \[\lim_{n \to \infty} n\sin\left(\frac{1}{n}\right)\]

Řešení

a) 3

b) 1

c) 0

d) $ \infty $

e) $ e^{-2} $

f) 1

7. Limity posloupností 1

Vypočítejte následující limity:

a) \[\lim_{n \to \infty} \frac{n}{n+1}\]

b) \[\lim_{n \to \infty} \frac{2n^2 + 3n}{n^2 + n}\]

c) \[\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n\]

d) \[\lim_{n \to \infty} \frac{\sin n}{n}\]

e) \[\lim_{n \to \infty} \frac{\sqrt{n^2 + 1}}{n+2}\]

f) \[\lim_{n \to \infty} \frac{n^2 + n + 1}{n^3 + 2n^2 + 3}\]

Řešení

a) 1

b) 2

c) e

d) 0

e) 1

f) 0

8. Determinant matice

Spočítejte determinant matice:

a) \[ A = \begin{pmatrix} 2 & 3 & 1 \\ 4 & 1 & -2 \\ 3 & 0 & 5 \end{pmatrix} \]

b) \[ B = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 0 & 1 \end{pmatrix} \]

Řešení

a) $ \text{det}(A) = -71 $

b) $ \text{det}(B) = 26 $

9. Soustavy rovnic Gaussovou eliminací

Pomocí Gaussovy eliminace řešte soustavy rovnic:

a) \[ \begin{pmatrix} 1 & 2 & -1 \\ 2 & 1 & 3 \\ 3 & -1 & 2 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ 5 \\ 4 \end{pmatrix} \]

b) \[ \begin{pmatrix} 2 & 3 & 1 \\ 4 & 7 & 3 \\ 6 & 9 & 5 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \]

c) \[ \begin{pmatrix} 1 & -1 & 2 \\ 3 & 2 & 1 \\ 2 & 1 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 4 \\ 7 \\ 1 \end{pmatrix} \]

d) \[ \begin{pmatrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 3 & 3 & 3 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 6 \\ 12 \\ 15 \end{pmatrix} \]

Řešení

a) $ x_1 = 1 $, $ x_2 = -1 $, $ x_3 = 1 $

b) $ x_1 = -1 $, $ x_2 = 0 $, $ x_3 = 1 $

c) $ x_1 = 1 $, $ x_2 = 1 $, $ x_3 = 2 $

d) Nemá řešení.

10. Derivace složených funkcí

Určete derivace následujících funkcí:

a) $ f_1(x) = \sin(3x^2) $

b) $ f_2(x) = \ln(\cos(x^2)) $

c) $ f_3(x) = e^{x^3} $

d) $ f_4(x) = \sqrt{2x^5 + 1} $

e) $ f_5(x) = \tan(\ln(x)) $

f) $ f_6(x) = \frac{1}{x^2 + e^{2x}} $

g) $ f_7(x) = \sin(\sqrt{x}) $

h) $ f_8(x) = \frac{\ln(x)}{x^3} $

Řešení

a) \[ f_1'(x) = \cos(3x^2) \cdot 6x \]

b) \[ f_2'(x) = -2x \cdot \tan(x^2)\]

c) \[ f_3'(x) = e^{x^3} \cdot 3x^2 \]

d) \[ f_4'(x) = \frac{5x^4}{\sqrt{2x^5 + 1}} \]

e) \[ f_5'(x) = \frac{1}{x \cdot \cos^2(\ln(x))} \]

f) \[ f_6'(x) = -\frac{2x + 2e^{2x}}{(x^2 + e^{2x})^2} \]

g) \[ f_7'(x) = \frac{\cos(\sqrt{x})}{2\sqrt{x}} \]

h) \[ f_8'(x) = \frac{1 - 3\ln(x)}{x^4} \]

11. Derivace polynomů

Určete derivace funkcí:

a) $ f_1(x) = 3x^4 - 5x^3 + 2x^2 - x + 7 $

b) $ f_2(x) = -2x^5 + 4x^4 - x^3 + 6x^2 - 3x $

c) $ f_3(x) = 5x^3 - 7x^2 + x - 8 $

d) $ f_4(x) = -x^5 + 3x^4 - 2x^2 + x - 4 $

e) $ f_5(x) = 6x^4 - 5x^3 + 4x - 9 $

f) $ f_6(x) = -4x^5 + x^3 - 3x^2 + 7x $

g) $ f_7(x) = 3x^4 - x^2 + 2x - 1 $

h) $ f_8(x) = 5x^5 - 3x^4 + x^2 - 6 $

Řešení

a) $ f'_1(x) = 12x^3 - 15x^2 + 4x - 1 $

b) $ f'_2(x) = -10x^4 + 16x^3 - 3x^2 + 12x - 3 $

c) $ f'_3(x) = 15x^2 - 14x + 1 $

d) $ f'_4(x) = -5x^4 + 12x^3 - 4x + 1 $

e) $ f'_5(x) = 24x^3 - 15x^2 + 4 $

f) $ f'_6(x) = -20x^4 + 3x^2 - 6x + 7 $

g) $ f'_7(x) = 12x^3 - 2x + 2 $

h) $ f'_8(x) = 25x^4 - 12x^3 + 2x $

12. Plocha pod křivkou

Najděte obsah plochy pod křivkou:

a) $ f(x) = 0.3x^2 + 0.2x - 0.2 $ v intervalu od $ x = 1 $ do $ x = 4 $,

b) $ f(x) = e^{-x} + 2 $ v intervalu od $ x = 0 $ do $ x = 2 $.

Řešení

a) Obsah plochy je $ 7.2 $ jednotek čtverečních.

b) Obsah plochy je přibližně $ 4.8647 $ jednotek čtverečních.

13. Determinant matic

Určete determinant matice:

a) \[ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \]

b) \[ \begin{pmatrix} 2 & 0 & 1 \\ 3 & 1 & 0 \\ 4 & 1 & 2 \end{pmatrix} \]

c) \[ \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 2 & 4 & 6 \end{pmatrix} \]

d) \[ \begin{pmatrix} 3 & 1 & 2 \\ 1 & 4 & 5 \\ 6 & 2 & 1 \end{pmatrix} \]

e) \[ \begin{pmatrix} 1 & 3 & 2 \\ 0 & 1 & 4 \\ 3 & 5 & 6 \end{pmatrix} \]

f) \[ \begin{pmatrix} 1 & 0 & 2 \\ 2 & 1 & 3 \\ 3 & 2 & 4 \end{pmatrix} \]

Řešení

a) 0

b) 3

c) 0

d) -33

e) 16

f) 0

14. Neurčitý integrál

Najděte určitý neurčitý integrál:

a) \[ \int x \cdot e^x \, dx \]

b) \[ \int \ln(x) \, dx \]

c) \[ \int x \cdot \cos(x) \, dx \]

d) \[ \int x \cdot \ln(x) \, dx \]

e) \[ \int x \cdot \sin(x) \, dx \]

f) \[ \int x^2 \cdot e^x \, dx \]

Řešení

a) \[ \int x \cdot e^x \, dx = e^x (x - 1) + C \]

b) \[ \int \ln(x) \, dx = x (\ln(x) - 1) + C \]

c) \[ \int x \cdot \cos(x) \, dx = x \cdot \sin(x) + \cos(x) + C \]

d) \[ \int x \cdot \ln(x) \, dx = \frac{x^2}{2} \cdot \ln(x) - \frac{x^2}{4} + C \]

e) \[ \int x \cdot \sin(x) \, dx = -x \cdot \cos(x) + \sin(x) + C \]

f) \[ \int x^2 \cdot e^x \, dx = e^x (x^2 - 2x + 2) + C \]

15. Průsečík dvou rovin

Jsou dány dvě roviny:

$ x + y - z = 0 $

$ -2x + y - z + 3 = 0 $

Určete průsečík těchto rovin.

Řešení

Průsečíkem rovin je přímka $ x + y - z = 0 $ a $ -2x + y - z + 3 = 0 $.

16. Řešení soustavy Gaussovou eliminací

Je dána soustava rovnic o 4 neznámých

\[ \begin{aligned} 3x_1 + 2x_2 - x_3 + 4x_4 &= 10 \\ x_1 - x_2 + 2x_3 - 3x_4 &= -5 \\ 4x_1 + 3x_2 + x_3 - x_4 &= 12 \\ 2x_1 + x_2 + 3x_3 + 2x_4 &= 7 \end{aligned} \]

Ověřte Frobeniovu podmínku a soustavu vyřešte pomocí Gaussovy eliminační metody.