Matikář - kategorie úloh

Úlohy: 1–5 / 5

Vyřešte goniometrické rovnice:

a) \[\sin x = \frac{1}{2}\]

b) \[\cos x = -\frac{\sqrt{2}}{2}\]

c) \[\tan x = \sqrt{3}\]

d) \[\sin^2 x = \frac{3}{4}\]

e) \[\cos 2x = 0\]

f) \[\tan^2 x = 3\]

a) \[x = \frac{\pi}{6} + 2k\pi \lor x = \frac{5\pi}{6} + 2k\pi, k \in \mathbb{Z}\]

b) \[x = \frac{3\pi}{4} + 2k\pi \lor x = \frac{5\pi}{4} + 2k\pi, k \in \mathbb{Z}\]

c) \[x = \frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]

d) \[x = \frac{\pi}{3} + 2k\pi \lor x = \frac{2\pi}{3} + 2k\pi \lor x = \frac{4\pi}{3} + 2k\pi \lor x = \frac{5\pi}{3} + 2k\pi, k \in \mathbb{Z}\]

e) \[x = \frac{\pi}{4} + \frac{k\pi}{2}, k \in \mathbb{Z}\]

f) \[x = \frac{\pi}{3} + k\pi \lor x = -\frac{\pi}{3} + k\pi, k \in \mathbb{Z}\]

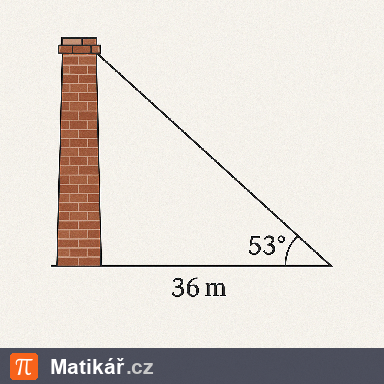
Ze vzdálenosti 36 metrů od paty komína je vidět jeho vršek pod úhlem 53º.

Vypočítejte v metrech výšku komína. Zaokrouhlete na jedno desetinné místo.

Výška komína je 47,80 m.

Vypočítejte zpaměti sin a cos uvedených úhlů:

a) $\frac{\pi}{4}$

b) $\frac{3\pi}{2}$

c) $150^\circ$

d) $30^\circ$

a) $\sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}; \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}$

b) $\sin\left(\frac{3\pi}{2}\right) = -1; \cos\left(\frac{3\pi}{2}\right) = 0$

c) $\sin(150^\circ) = \frac{1}{2}; \cos(150^\circ) = -\frac{\sqrt{3}}{2}$

d) $\sin(30^\circ) = \frac{1}{2}; \cos(30^\circ) = \frac{\sqrt{3}}{2}$

Z rozhledny, která je 15 m vysoká a od řeky vzdálená 30 m, vidíme řeku pod výškovým úhlem 15 °.

Vypočtěte šířku řeky v metrech a zapište na jedno desetinné místo.

Řeka je široká 43,30 metrů.

Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15 °.

Vypočtěte, kolik metrů je řeka široká.

Řeka je široká 43,30 m.