Úlohy: 1–20 / 26

12
Přehled ročníků

1. Kružnice opsaná a vepsaná

Je dán čtverec o obsahu 36 cm2.

Vypočítejte v centimetrech poloměr
a)   kružnice vepsaná,
b)   kružnice opsané.
Řešení
a)   Poloměr kružnice vepsané je 3 cm.
b)   Poloměr kružnice opsané je přibližně 4,24 cm.
Matematická úloha – Kružnice opsaná a vepsaná

2. Žebřík opřený o stěnu

Žebřík má délku 8 metrů. Je opřen o stěnu tak, že jeho dolní konec je ode stěny vzdálen 1,50 metru.

Vypočítejte, do jaké výšky stěny dosahuje žebřík. (Výsledek zapište na dvě desetinná místa.)
Řešení
Žebřík dosahuje do výšky 7,86 metru.
Matematická úloha – Žebřík opřený o stěnu

3. Lanovka na horách

Lanovka má délku 1 500 metrů. Vodorovná vzdálenost horní a dolní stanice lanovky je 1 200 metrů.

Vypočítej, o kolik metrů je horní stanice výš než dolní stanice.
Řešení
Horní stanice lanovky je o 900 metrů výše než dolní stanice.
Matematická úloha – Lanovka na horách

4. Délka výztuhy rámu

Tesař vyrábí pravoúhlý trojúhelníkový rám na dveře. Jedna strana rámu (výška) měří 150 cm a druhá strana rámu (šířka) měří 200 cm. Tesař potřebuje zjistit délku úhlopříčky rámu (přepony), aby mohl připravit správnou výztuhu.

Vypočítejte, kolik centimetrů dlouhá má být úhlopříčka (výztuha).
Řešení
Délka úhlopříčky rámu musí být 250 cm.
Matematická úloha – Délka výztuhy rámu

5. Vlastnosti rovnoramenného trojúhelníku

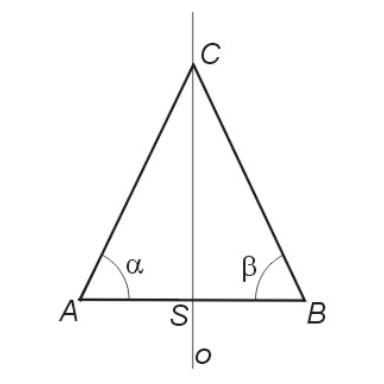
V rovnoramenném trojúhelníku je délka ramene 25 cm, výška trojúhelníku je 24 cm.

Vypočítejte:
a)   délku základny v centimetrech,
b)   obvod trojúhelníku v centimetrech,
c)   obsah trojúhelníku v centimetrech čtverečných.
Řešení
a)   Délka základny je 14 cm.
b)   Obvod trojúhelníku je 64 cm.
c)   Obsah trojúhelníku je 168 cm².
Matematická úloha – Vlastnosti rovnoramenného trojúhelníku

6. Cesty v parku

Cesty v parku tvoří pravoúhlý trojúhelník, jehož odvěsny mají na plánku s měřítkem 1:200 rozměry délek stran 9 cm a 12 cm. Babička chodí každý den po této trase na zdravotní procházku.

Vypočítejte
a)   kolik m2 zabírá plocha ohraničená těmito cestami,
b)   kolikrát musí babička projít všechny tři cesty, aby nachodila alespoň 1,50 km.
Řešení
Matematická úloha – Cesty v parku

7. Jakub a Filip na křižovatce

Jakub a Filip, každý na svém jízdním kole, stáli na křižovatce, kde se křížily kolmé ulice. Jakub se vydal jednou ulicí rychlostí 12 km/h, Filip druhou ulicí rychlostí 16 km/hod.

Vypočítejte, jak daleko od sebe byli za 15 minut od startu.
Řešení
Po 15 minutách od startu jsou Jakub a Filip od sebe vzdáleni 5 km.
Matematická úloha – Jakub a Filip na křižovatce

8. Šestiboký jehlan

Pravidelný šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm.

Vypočítejte v cm3 objem jehlanu. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Objem jehlanu je 5 196,15 cm3
Matematická úloha – Šestiboký jehlan

9. Pravoúhlý trojúhelník

Pravoúhlý trojúhelník má obvod 36 cm. Přepona je o 6 cm delší než kratší z odvěsen.

Vypočítejte délky stran trojúhelníka.
Řešení
Velikost kratší z odvěsen je 9 cm, velikost delší z odvěsen je 12 cm, velikost přepony je 15 cm.
Matematická úloha – Pravoúhlý trojúhelník

10. Pravidelný čtyřboký jehlan

Objem pravidelného čtyřbokého jehlanu je 288 dm³. Obvod jeho podstavy je stejně velký jako jeho výška.

Vypočítejte v dm² povrch jehlanu. (Výsledek zaokrouhlete na celé dm².)
Řešení
Povrch jehlanu je 326 dm².
Matematická úloha – Pravidelný čtyřboký jehlan

11. Pozemek tvaru lichoběžníku

Pozemek tvaru pravoúhlého lichoběžníku má základny dlouhé 102 m a 86 m. Kolmé rameno má délku 63 m.

Vypočítejte
a)   obsah pozemku,
b)   obvod pozemku.
Řešení
a)   Obsah pozemku je 5 922 m2m
b)   obvod pozemku 316 metrů.
Matematická úloha – Pozemek tvaru lichoběžníku

12. Pravoúhlý trojúhelník

Délky stran pravoúhlého trojúhelníku tvoří první 3 členy aritmetické posloupnosti. Obsah trojúhelníku je 600 cm2.

Určete délky stran trojúhelníku.
Řešení
Délky stran trojúhelníku podle velikosti jsou 30 cm, 40 cm a 50 cm.
Matematická úloha – Pravoúhlý trojúhelník

13. Obsahy trojúhelníků

Obsah pravoúhlého trojúhelníku KLM s pravým úhlem u vrcholu L je S = 60 cm2 a jeho odvěsna |LM|=10 cm. Trojúhelníky KLM a RST jsou podobné, poměr podobnosti je k = 2,5.

Vypočítejte obsah trojúhelníku RST.
Řešení
Obsah trojúhelníku RST je 375 cm2.
Matematická úloha – Obsahy trojúhelníků

14. Sestrojení obdélníku

Je dán obdélník ABCD: |AB| = 8 cm a délka úhlopříčky |AC| = 13 cm.

Sestrojte obdélník ABCD.
Řešení
Matematická úloha – Sestrojení obdélníku

15. Rozměry televize

Úhlopříčka televizní obrazovky je dlouhá 105 cm. Poměr stran je 4:3.

Vypočítejte, kolik centimetrů měří kratší strana.
Řešení
Délka kratší strany je 63 cm.
Matematická úloha – Rozměry televize

16. Úhlopříčka ve čtverci

Čtverec má uhlopříčku délky 3 metry.

a)   Vypočítejte, kolik centimetrů je jeho strana. (Zaokrouhlete na dvě desetinná místa.)
b)   
Řešení
Délka strany čtverce je dlouhá přibližně 212,13 centimetrů.
Matematická úloha – Úhlopříčka ve čtverci

17. Trám z klády

Kmen má průměr 20 centimetrů. Truhlář z něj chce vyrobit čtvercový trám.

Vypočítejte, kolik centimetrů je největší možná délka hrany takového čtverce. (Zaokrouhlete na dvě desetinná čísla.)
Řešení
Délka strany čtverce je přibližně (14.14) centimetrů.
Matematická úloha – Trám z klády

18. Žebřík opřený o zeď

Žebřík se dotýká zdi ve výšce 4 metry, spodní konec je 1,50 metru od zdi.

Vypočítejte, kolik metrů měří žebřík. (Zaokrouhlete na 2 desetinná místa.)
Řešení
Takže délka žebříku je přibližně \(4.27\) metrů.
Matematická úloha – Žebřík opřený o zeď

19. Pochod z křižovatky

Na křižovatce dvou kolmých cest se rozdělila skupina turistů. Jedna skupina šla rychlostí 5,3 km/h. Druhá skupina 4,1 km/h.

Vypočtěte, kolik kilometrů byly od sebe obě skupiny vzdáleny po 1 h 25 min. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Skupiny turistů byly od sebe vzdáleny 9,49 km.

20. Vychýlená věž

Výška věže je 56 m a vrchol věže se nachází ve výšce 55,86 m.

Určete, o kolik metrů je věž vychýlená. (Zaokrouhlete na dvě desetinná místa.)
Řešení
Věž je vychýlená o 4,03 m.
Matematická úloha – Vychýlená věž
 
12